Giải bài tập 6.21 trang 20 SGK Toán 9 tập 2 - Kết nối tri thức
Từ một tấm tôn hình vuông, người ta cắt bỏ bốn hình vuông có độ dài cạnh 8cm ở bốn góc, sau đó gập thành một chiếc thùng có dạng hình hộp chữ nhật không có nắp và có thể tích là (200c{m^3}). Tính độ dài cạnh của tấm tôn hình vuông ban đầu.
Đề bài
Từ một tấm tôn hình vuông, người ta cắt bỏ bốn hình vuông có độ dài cạnh 8cm ở bốn góc, sau đó gập thành một chiếc thùng có dạng hình hộp chữ nhật không có nắp và có thể tích là \(200c{m^3}\). Tính độ dài cạnh của tấm tôn hình vuông ban đầu.
Phương pháp giải - Xem chi tiết
+ Gọi độ dài cạnh miếng tôn hình vuông ban đầu là x, đặt điều kiện.
+ Tính các kích thước của hình hộp chữ nhật theo x.
+ Tính thể tích của hình hộp chữ nhật theo x.
+ Lập phương trình ẩn về thể tích theo x, giải phương trình, đối chiếu điều kiện và đưa ra kết luận.
Lời giải chi tiết
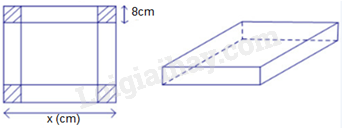
Gọi độ dài cạnh của tấm tôn ban đầu là x (cm, \(x > 16\)).
Khi cắt bỏ bốn hình vuông có độ dài cạnh 8cm ở bốn góc và gập lại, thu được một hình hộp chữ nhật có độ dài các cạnh đáy lần lượt là \(x - 16;x - 16\) và chiều cao là 8cm.
Do đó, thể tích của hình hộp chữ nhật là: \(8{\left( {x - 16} \right)^2}\;\left( {c{m^3}} \right)\)
Mà thể tích của hình hộp chữ nhật là \(200c{m^3}\) nên ta có: \(8{\left( {x - 16} \right)^2} = 200\)
\({\left( {x - 16} \right)^2} = 25\)
\(x - 16 = 5\) hoặc \(x - 16 = - 5\)
\(x = 21\left( {tm} \right)\) hoặc \(x = 11\left( {ktm} \right)\)
Vậy độ dài của cạnh hình vuông ban đầu là 21cm.