Giải bài tập 6 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho tam giác ABC vuông tại A. Lấy điểm M bất kì trên đoạn AC, đường tròn đường kính CM cắt hai đường thẳng BM và BC lần lượt tại D và N. Chứng minh rằng: a) Tứ giác ABCD nội tiếp; b) Các đường thẳng AB, MN, CD cùng đi qua một điểm.
Đề bài
Cho tam giác ABC vuông tại A. Lấy điểm M bất kì trên đoạn AC, đường tròn đường kính CM cắt hai đường thẳng BM và BC lần lượt tại D và N. Chứng minh rằng:
a) Tứ giác ABCD nội tiếp;
b) Các đường thẳng AB, MN, CD cùng đi qua một điểm.
Phương pháp giải - Xem chi tiết
- Đọc kĩ dữ liệu để vẽ hình.
- Dựa vào góc nội tiếp chắn nửa đường tròn bằng 90 o và trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180 o để suy ra tứ giác ABCD nội tiếp.
- Chứng minh AB, MN, CD là ba đường cao của tam giác MBC suy ra các đường thẳng AB, MN, CD cùng đi qua điểm E.
Lời giải chi tiết
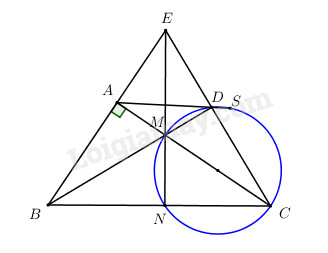
a) Ta có \(\widehat {MDC} = {90^o}\)(góc nội tiếp chắn nửa đường tròn đường kính MC)
Xét tứ giác ABCD ta có \(\widehat {BAC} = {90^o};\widehat {BDC} = {90^o}\)
Suy ra A, D thuộc đường tròn đường kính BC.
Vậy tứ giác ABCD nội tiếp.
b) Ta có \(\widehat {MNC} = {90^o}\) (góc nội tiếp chắn nửa đường tròn đường kính MC)
Xét tam giác MBC có AB \( \bot \) MC, CD \( \bot \) BM, MN \( \bot \) BC.
Nên AB, MN, CD là ba đường cao của tam giác MBC
Vậy các đường thẳng AB, MN, CD cùng đi qua điểm E.