Giải bài tập 7. 11 trang 38 SGK Toán 9 tập 2 - Cùng khám phá — Không quảng cáo

Đề bài

Cho ABCD là tứ giác nội tiếp.

a) Chứng minh rằng $\widehat {BAC} = \widehat {BDC}$ .

b) AC cắt BD tại M. Chứng minh rằng MA.MC = MB.MD.

Lời giải chi tiết

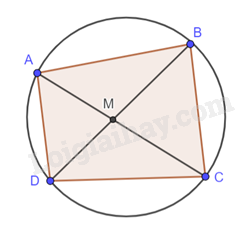
a) Ta có $\widehat {BAC}$ và $\widehat {BDC}$ là hai góc nội tiếp cùng chắn cung BC nhỏ nên $\widehat {BAC} = \widehat {BDC}$.

b) Xét $\Delta$BAM và $\Delta$CDM có

$\widehat {BAM} = \widehat {MDC}$ (cmt)

$\widehat {AMB} = \widehat {CMD}$ (đối đỉnh)

Suy ra $\Delta$BAM $\backsim$ $\Delta$CDM (g-g)

Nên $\frac{{MA}}{{MB}} = \frac{{MD}}{{MC}}$ hay MA.MC = MB.MD.