Giải bài tập 7.13 trang 38 SGK Toán 9 tập 2 - Cùng khám phá
Trong Hình 7.22, ABCD là tứ giác nội tiếp. Tính số đo các góc x, y, z.
Đề bài
Trong Hình 7.22, ABCD là tứ giác nội tiếp. Tính số đo các góc x, y, z.
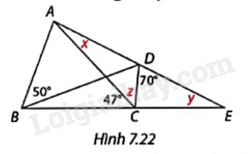
Phương pháp giải - Xem chi tiết
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\) và góc bẹt bằng \({180^o}\) .
Lời giải chi tiết
Ta có ABCD nội tiếp nên \(\widehat {ADB} = \widehat {ACB} = {47^o}\) (góc nội tiếp cùng chắn cung AB)
Ta có \(\widehat {ADE} = {180^o}\) (góc bẹt) nên
\(\widehat {ADC} = {180^o} - \widehat {EDC} = {180^o} - {70^o} = {110^o}\)
Vì ABCD nội tiếp nên
\(\widehat {ABC} = {180^o} - {110^o} = {70^o}\)
suy ra \(\widehat {DBC} = {70^o} - {50^o} = {20^o}\)
Ta có \(x =\widehat {DAC} = \widehat {DBC} = {20^o}\) (góc nội tiếp cùng chắn cung CD)
Xét tam giác ADC ta có
\(z = \widehat {ACD} = {180^o} - \left( {\widehat {ADC} + \widehat {CAD}} \right) = {180^o} - \left( {{{110}^o} + {{20}^o}} \right) = {50^o}\)
Ta có \(\widehat {BCE} = {180^o}\) (góc bẹt) nên \(\widehat {DCE} = {180^o} - \left( {\widehat {BCA} + \widehat {ACD}} \right) = {180^o} - \left( {{{47}^o} + {{50}^o}} \right) = {83^o}\)
Xét tam giác CDE có
\(y = \widehat {DEC} = {180^o} - \left( {\widehat {CDE} + \widehat {DCE}} \right) = {180^o} - \left( {{{70}^o} + {{83}^o}} \right) = {27^o}\).