Giải bài tập 7 trang 90 SGK Toán 12 tập 2 - Kết nối tri thức
Cho hàm số f(x) liên tục trên \(\mathbb{R}\). Gọi S là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = 0,x = - 1\) và \(x = 4\) như hình bên. Khẳng định nào dưới đây là đúng? A. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \). B. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \). C. \(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \).
Đề bài
Cho hàm số f(x) liên tục trên \(\mathbb{R}\). Gọi S là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = 0,x = - 1\) và \(x = 4\) như hình bên.
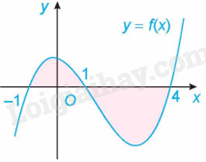
Khẳng định nào dưới đây là đúng?
A. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \).
B. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \).
C. \(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \).
D. \(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và đường thẳng \(x = a,x = b\) để tính: Diện tích S của hình phẳng giới hạn đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng \(x = a,x = b\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết
Diện tích hình phẳng cần tính là: \(S = \int\limits_{ - 1}^4 {\left| {f\left( x \right) - 0} \right|dx} = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \)
Chọn B