Giải mục 1 trang 12, 13 SGK Toán 12 tập 2 - Chân trời sáng tạo — Không quảng cáo

KP1

Trả lời câu hỏi Khám phá 1 trang 12 SGK Toán 12 Chân trời sáng tạo

Cho hàm số $y = f\left( x \right) = x + 1$. Với mỗi $x \ge 1$, kí hiệu $S\left( x \right)$ là diện tích của hình thang giới hạn bởi đồ thị hàm số $y = f\left( x \right)$, trục hoành và hai đường thẳng vuông góc với $Ox$ tại các điểm có hoành độ 1 và $x$.

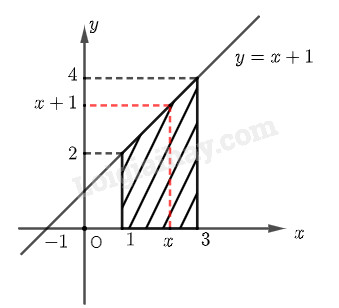
a) Tính $S\left( 3 \right)$.

b) Tính $S\left( x \right)$ với mỗi $x \ge 1$.

c) Tính $S'\left( x \right)$. Từ đó suy ra $S\left( x \right)$ là một nguyên hàm của $f\left( x \right)$ trên $\left[ {1; + \infty } \right)$.

d) Cho $F\left( x \right)$ là một nguyên hàm của hàm số $f\left( x \right)$. Chứng tỏ rằng $F\left( 3 \right) - F\left( 1 \right) = S\left( 3 \right)$. Từ đó nhận xét về cách tính $S\left( 3 \right)$ khi biết một nguyên hàm của $f\left( x \right)$.

Phương pháp giải:

a, b) Gọi các điểm $A$, $B$, $C$, $D$ là các đỉnh của hình thang như hình vẽ. Tính độ dài các cạnh $AD$, $BC$ và $AB$, rồi sử dụng công thức tính diện tích hình thang ${S_{ABCD}} = \frac{{\left( {AD + BC} \right).AB}}{2}$ để tính $S\left( 3 \right)$ ở câu a và $S\left( x \right)$ ở câu b.

c) Sử dụng công thức đạo hàm để tính $S'\left( x \right)$ và kết luận.

d) Tính nguyên hàm của $f\left( x \right)$, sau đó tính $F\left( 3 \right) - F\left( 1 \right)$, so sánh với $S\left( 3 \right)$

Lời giải chi tiết:

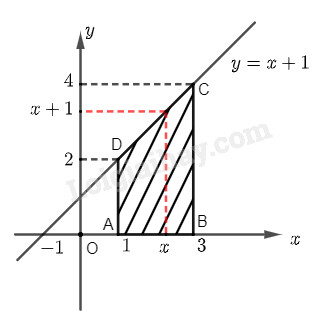
a) Gọi các điểm $A$, $B$, $C$, $D$ là các đỉnh của hình thang như hình vẽ. Dễ thấy rằng $ABCD$ là hình thang vuông có hai đáy là $AD$ và $BC$, chiều cao là $AB$.

Ta có $AB = 3 - 1 = 2$, $AD = 2$ và $BC = 4$. Do đó diện tích hình thang $ABCD$ là:

$S\left( 3 \right) = \frac{{\left( {2 + 4} \right).2}}{2} = 6$.

b) Tương tự câu a, nhưng hoành độ của $B$ là $x$, ta suy ra tung độ của $C$ là $x + 1$.

Ta có $AB = x - 1$, $AD = 2$, $BC = x + 1$. Do đó diện tích hình thang $ABCD$ là:

$S\left( x \right) = \frac{{\left( {AD + BC} \right).AB}}{2} = \frac{{\left( {2 + x + 1} \right)\left( {x - 1} \right)}}{2} = \frac{{\left( {x + 3} \right)\left( {x - 1} \right)}}{2} = \frac{{{x^2} + 2x - 3}}{2}$

c) Ta có $S'\left( x \right) = \frac{{2x + 2}}{2} = x + 1 = f\left( x \right)$. Vậy $S\left( x \right)$ là một nguyên hàm của $f\left( x \right)$.

d) Do $F\left( x \right)$ là một nguyên hàm của $f\left( x \right)$, ta có:

$F\left( x \right) = \int {f\left( x \right)dx}  = \int {\left( {x + 1} \right)dx}  = \frac{{{x^2}}}{2} + x + C$

Suy ra $F\left( 3 \right) = \frac{{{3^2}}}{2} + 3 + C = \frac{{15}}{2} + C$ và $F\left( 1 \right) = \frac{{{1^2}}}{2} + 1 + C = \frac{3}{2} + C$

Như vậy ta có $F\left( 3 \right) - F\left( 1 \right) = \left( {\frac{{15}}{2} + C} \right) - \left( {\frac{3}{2} + C} \right) = 6 = S\left( 3 \right)$.

Do đó, để tính $S\left( 3 \right)$ khi biết một nguyên hàm của $f\left( x \right)$, ta thực hiện tính nguyên hàm $F\left( x \right)$ của $f\left( x \right)$, sau đó ta tính $F\left( 3 \right)$ và $F\left( 1 \right)$, từ đó tính được $S\left( 3 \right) = F\left( 3 \right) - F\left( 1 \right)$.

TH1

Trả lời câu hỏi Thực hành 1 trang 13 SGK Toán 12 Chân trời sáng tạo

Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số $y = f\left( x \right) = {e^x}$, trục hoành, trục tung và đường thẳng $x = 1$.

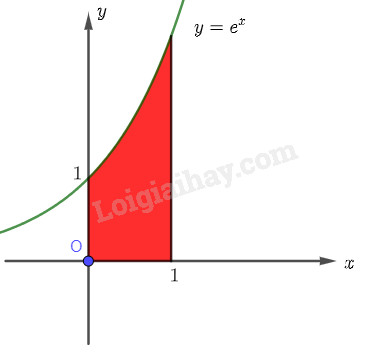
Phương pháp giải:

Tìm một nguyên hàm $F\left( x \right)$ của hàm số $f\left( x \right)$, sau đó sử dụng công thức để tính diện tích hình thang cong $S = F\left( b \right) - F\left( a \right)$.

Lời giải chi tiết:

Ta có hàm số $y = f\left( x \right) = {e^x}$ liên tục và dương trên đoạn $\left[ {0;1} \right]$.

Ta có $\int {f\left( x \right)dx}  = \int {{e^x}dx}  = {e^x} + C$, từ đó suy ra $F\left( x \right) = {e^x}$ là một nguyên hàm của $f\left( x \right) = {e^x}$.

Diện tích hình thang cong cần tính là: $S = F\left( 1 \right) - F\left( 0 \right) = {e^1} - {e^0} = e - 1$.