Giải mục 1 trang 21, 22, 23 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tính diện tích hình phẳng
KP1
Trả lời câu hỏi Khám phá 1 trang 21 SGK Toán 12 Chân trời sáng tạo
Gọi \(d\) là đồ thị của hàm số \(y = f\left( x \right) = 6 - 2x\). Kí hiệu \({S_1}\) là diện tích hình phẳng giới hạn bởi \(d\), trục hoành và trục tung; \({S_2}\) là diện tích hình phẳng giới hạn bởi \(d\), trục hoành và đường thẳng \(x = 5\) (Hình 1).
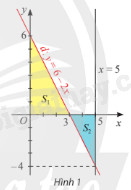
a) Tính \({S_1}\) và so sánh với \(\int\limits_0^3 {f\left( x \right)dx} \).
b) Tính \({S_2}\) và so sánh với \(\int\limits_3^5 {f\left( x \right)dx} \).
c) So sánh \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} \) với \({S_1} + {S_2}\).
Phương pháp giải:
a) Theo hình vẽ, \({S_1}\) là diện tích tam giác \(OAB\). Tính diện tích tam giác \(OAB\), sau đó tính tích phân \(\int\limits_0^3 {f\left( x \right)dx} \) và so sánh các kết quả thu được.
b) Theo hình vẽ. \({S_2}\) là diện tích tam giác \(CBM\). Tính diện tích tam giác \(CBM\), sau đó tính tích phân \(\int\limits_3^5 {f\left( x \right)dx} \) và so sánh các kết quả thu được.
c) Tính \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = \int\limits_0^3 {\left| {f\left( x \right)} \right|dx} + \int\limits_3^5 {\left| {f\left( x \right)} \right|dx} \), sau đó phá dấu giá trị tuyệt đối và tính các tích phân cơ bản, sau đó so sánh kết quả thu được với \({S_1} + {S_2}\).
Lời giải chi tiết:
a) Tam giác \(OAB\) vuông tại \(O\), ta có \(OA = 6\), \(OB = 3\). Diện tích tam giác \(OAB\) là:
\({S_1} = \frac{{OA.OB}}{2} = \frac{{6.3}}{2} = 9\).
Ta có \(\int\limits_0^3 {f\left( x \right)dx} = \int\limits_0^3 {\left( {6 - 2x} \right)dx} = \left. {\left( {6x - {x^2}} \right)} \right|_0^3 = 9 - 0 = 9\).
Như vậy \({S_1} = \int\limits_0^3 {f\left( x \right)dx} \)
b) Tam giác \(CBM\) vuông tại \(M\), ta có \(MB = 2\), \(MC = 4\). Diện tích tam giác \(CBM\) là:
\({S_2} = \frac{{MB.MC}}{2} = \frac{{2.4}}{2} = 4\).
Ta có \(\int\limits_0^3 {f\left( x \right)dx} = \int\limits_3^5 {\left( {6 - 2x} \right)dx} = \left. {\left( {6x - {x^2}} \right)} \right|_3^5 = 5 - 9 = - 4\).
Như vậy \({S_2} = - \int\limits_3^5 {f\left( x \right)dx} \)
c) Ta có:
\(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = \int\limits_0^5 {\left| {6 - 2x} \right|dx} = \int\limits_0^3 {\left| {6 - 2x} \right|dx} + \int\limits_3^5 {\left| {6 - 2x} \right|dx} = \int\limits_0^3 {\left( {6 - 2x} \right)dx} + \int\limits_3^5 {\left( {2x - 6} \right)dx} \)
\( = \left. {\left( {6x - {x^2}} \right)} \right|_0^3 + \left. {\left( {{x^2} - 6x} \right)} \right|_3^5 = \left( {9 - 0} \right) + \left[ {\left( { - 5} \right) - \left( { - 9} \right)} \right] = 13\)
Như vậy \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = 13 = {S_1} + {S_2}\).
TH1
Trả lời câu hỏi Thực hành 1 trang 22 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = 2x - {x^2}\), trục hoành và hai đường thẳng \(x = 0\), \(x = 3\).
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = 2x - {x^2}\), trục hoành và hai đường thẳng \(x = 0\), \(x = 3\) là \(S = \int\limits_0^3 {\left| {2x - {x^2}} \right|dx} \)
Ta có \(2x - {x^2} = 0 \Leftrightarrow x = 0\) hoặc \(x = 2\).
Với \(x \in \left[ {0;2} \right]\) thì \(2x - {x^2} \ge 0\). Với \(x \in \left[ {2;3} \right]\) thì \(2x - {x^2} \le 0\).
Vậy \(S = \int\limits_0^3 {\left| {2x - {x^2}} \right|dx} = \int\limits_0^2 {\left( {2x - {x^2}} \right)dx} + \int\limits_2^3 {\left( {{x^2} - 2x} \right)dx} \)
\( = \left. {\left( {{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^2 + \left. {\left( {\frac{{{x^3}}}{3} - {x^2}} \right)} \right|_2^3 = \left( {\frac{4}{3} - 0} \right) + \left[ {0 - \left( { - \frac{4}{3}} \right)} \right] = \frac{8}{3}\)
TH2
Trả lời câu hỏi Thực hành 2 trang 22 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = \cos x - 2\), trục hoành và hai đường thẳng \(x = 0\), \(x = \pi \).
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = \cos x - 2\), trục hoành và hai đường thẳng \(x = 0\), \(x = \pi \) là \(S = \int\limits_0^\pi {\left| {\cos x - 2} \right|dx} \).
Do \(\cos x - 2 < 0\) với \(\forall x \in \left[ {0;\pi } \right]\).
Do đó \(S = \int\limits_0^\pi {\left( {2 - \cos x} \right)dx} = \left. {\left( {2x - \sin x} \right)} \right|_0^\pi = 2\pi - 0 = 2\pi \).
KP2
Trả lời câu hỏi Khám phá 2 trang 23 SGK Toán 12 Chân trời sáng tạo
Cho hai hàm số \(y = 4x - {x^2}\) và \(y = x\) lần lượt có đồ thị \(\left( P \right)\) và \(d\) như hình 4.
a) Tính diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\).
b) Tính diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\).
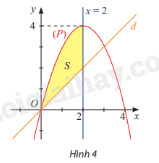
Phương pháp giải:
a) Diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_1} = \int\limits_0^2 {\left| {4x - {x^2}} \right|dx} \)
b) Diện tích \({S_2}\) của hình phẳng giới hạn bởi \(d\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_2} = \int\limits_0^2 {\left| x \right|dx} \).
Suy ra diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\) là \(S = {S_1} - {S_2}\).
Lời giải chi tiết:
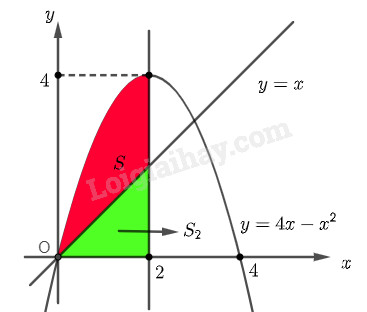
Diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_1} = \int\limits_0^2 {\left| {4x - {x^2}} \right|dx} \)
Ta thấy rằng với \(\forall x \in \left[ {0;2} \right]\) thì \(4x - {x^2} \ge 0\), do đó:
\({S_1} = \int\limits_0^2 {\left( {4x - {x^2}} \right)dx} = \left. {\left( {2{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^2 = \frac{{16}}{3}\)
b) Diện tích \({S_2}\) của hình phẳng giới hạn bởi \(d\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_2} = \int\limits_0^2 {\left| x \right|dx} \).
Ta thấy rằng với \(\forall x \in \left[ {0;2} \right]\) thì \(x \ge 0\), do đó:
\({S_2} = \int\limits_0^2 {xdx} = \left. {\left( {\frac{{{x^2}}}{2}} \right)} \right|_0^2 = 2\)
Vậy diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\) là \(S = {S_1} - {S_2} = \frac{{16}}{3} - 2 = \frac{{10}}{3}\).
TH3
Trả lời câu hỏi Thực hành 3 trang 24 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2} - 2x - 1\), \(y = x - 1\) và hai đường thẳng \(x = 1\), \(x = 4\).
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \({f_1}\left( x \right)\) và \({f_2}\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và hai đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \)
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2} - 2x - 1\), \(y = x - 1\) và hai đường thẳng \(x = 1\), \(x = 4\) là:
\(S = \int\limits_1^4 {\left| {\left( {{x^2} - 2x - 1} \right) - \left( {x - 1} \right)} \right|dx} = \int\limits_1^4 {\left| {{x^2} - 3x} \right|dx} \)
Ta có \({x^2} - 3x = 0 \Leftrightarrow x = 0\) hoặc \(x = 3\)
Do đó
\(S = \int\limits_1^3 {\left| {{x^2} - 3x} \right|dx} + \int\limits_3^4 {\left| {{x^2} - 3x} \right|dx} = \left| {\int\limits_1^3 {\left( {{x^2} - 3x} \right)dx} } \right| + \left| {\int\limits_3^4 {\left( {{x^2} - 3x} \right)dx} } \right|\)
\( = \left| {\left. {\left( {\frac{{{x^3}}}{3} - 3\frac{{{x^2}}}{2}} \right)} \right|_1^3} \right| + \left| {\left. {\left( {\frac{{{x^3}}}{3} - 3\frac{{{x^2}}}{2}} \right)} \right|_3^4} \right| = \left| {\frac{{ - 9}}{2} - \frac{{ - 7}}{6}} \right| + \left| {\frac{{ - 8}}{3} - \frac{{ - 9}}{2}} \right| = \left| { - \frac{{10}}{3}} \right| + \left| {\frac{{11}}{6}} \right| = \frac{{31}}{6}\)
TH4
Trả lời câu hỏi Thực hành 4 trang 24 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = 5x - {x^2}\), \(y = {x^2} - x\) và hai đường thẳng \(x = 0\), \(x = 2\).
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \({f_1}\left( x \right)\) và \({f_2}\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và hai đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \)
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = 5x - {x^2}\), \(y = {x^2} - x\) và hai đường thẳng \(x = 0\), \(x = 2\) là
\(S = \int\limits_0^2 {\left| {\left( {5x - {x^2}} \right) - \left( {{x^2} - x} \right)} \right|dx} = \int\limits_0^2 {\left| {6x - 2{x^2}} \right|dx} = 2\int\limits_0^2 {\left| {{x^2} - 3x} \right|dx} \)
Ta có \({x^2} - 3x = 0 \Leftrightarrow x = 0\) hoặc \(x = 3\)
Do đó \(S = \left| {\int\limits_0^2 {\left( {{x^2} - 3x} \right)dx} } \right| = \left| {\left. {\left( {\frac{{{x^3}}}{3} - 3\frac{{{x^2}}}{2}} \right)} \right|_0^2} \right| = \left| { - \frac{{10}}{3}} \right| = \frac{{10}}{3}\)
VD1
Trả lời câu hỏi Vận dụng 1 trang 24 SGK Toán 12 Chân trời sáng tạo
Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như hình 7. Tính diện tích của cửa hầm.
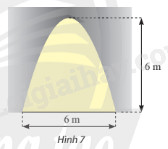
Phương pháp giải:
Ta ghép mặt cắt của cửa hầm vào mặt phẳng \(Oxy\) như hình vẽ dưới đây.
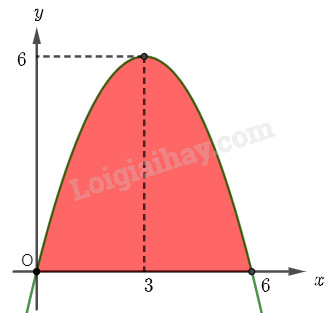
Diện tích của cửa hầm chính là diện tích phần mặt phẳng giới hạn bởi parabol \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = 0\) và \(x = 6\).
Để tính được diện tích của cửa hầm, ta xác định phương trình của parabol \(y = f\left( x \right)\) như trong hình, sau đó tính tích phân \(S = \int\limits_0^6 {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Ta ghép mặt cắt của cửa hầm vào mặt phẳng \(Oxy\) như hình vẽ dưới đây. Diện tích của cửa hầm chính là diện tích hình phẳng giới hạn bởi parabol \(y = f\left( x \right) = a{x^2} + bx + c\), trục hoành và hai đường thẳng \(x = 0\), \(x = 6\).
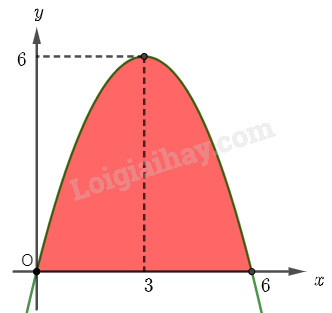
Ta nhận thấy rằng parabol đi qua các điểm có toạ độ \(\left( {0;0} \right)\), \(\left( {6;0} \right)\) và \(\left( {3;6} \right)\) (trục đối xứng của parabol đi qua đỉnh), do đó ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{a{{.0}^2} + b.0 + c = 0}\\{a{{.6}^2} + b.6 + c = 0}\\{a{{.3}^2} + b.3 + c = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{36a + 6b + c = 0}\\{9a + 3b + c = 6}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - \frac{2}{3}}\\{b = 4}\\{c = 0}\end{array}} \right.} \right.\)
Vậy phương trình của parabol là \(y = - \frac{2}{3}{x^2} + 4x\).
Ta thấy rằng với \(x \in \left[ {0;6} \right]\) thì parabol nằm trên trục hoành. Do đó, diện tích của cửa hầm, cũng chính là diện tích hình phẳng giới hạn bởi parabol \(y = - \frac{2}{3}{x^2} + 4x\), trục hoành và các đường thẳng \(x = 0\), \(x = 6\) là:
\(S = \int\limits_0^6 {\left| { - \frac{2}{3}{x^2} + 4x} \right|dx} = \int\limits_0^6 {\left( { - \frac{2}{3}{x^2} + 4x} \right)dx} = \left. {\left( {\frac{{ - 2}}{9}{x^3} + 2{x^2}} \right)} \right|_0^6 = 24\)
Vậy diện tích của cửa hầm là 24 \({{\rm{m}}^2}\).