Giải mục 1 trang 6, 7, 8 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tính đơn điệu của hàm số
TH1
Trả lời câu hỏi Thực hành 1 trang 7 SGK Toán 12 Chân trời sáng tạo
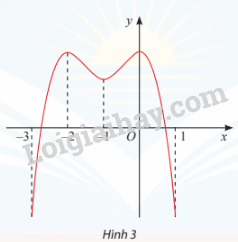
Tìm các khoảng đơn điệu của hàm số y = f(x) có đồ thị cho ở Hình 3.
Phương pháp giải:
Hàm số y = f(x) gọi là đồng biến (tăng) trên K nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1}\) < \({x_2}\) thì f(\({x_1}\)) < f(\({x_2}\)). Hàm số y = f(x) gọi là nghịch biến (giảm) trên K nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1}\) < \({x_2}\) thì f(\({x_1}\)) > f(\({x_2}\)).
Lời giải chi tiết:
Hàm số đồng biến trên các khoảng (−3; -2) và (-1; 0)
Hàm số nghịch biến trên khoảng (-2; -1) và (0; 1)
KP1
Trả lời câu hỏi Khám phá 1 trang 7 SGK Toán 12 Chân trời sáng tạo
Cho hàm số y = f(x) = \({x^2}\)
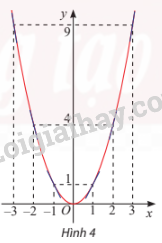
a) Từ đồ thị của hàm số y = f(x) (Hình 4), hãy chỉ ra các
khoảng đồng biến và nghịch biến của hàm số đã cho.
b) Tính đạo hàm f '(x) và xét dấu f '(x).
c) Từ đó, nhận xét về mối liên hệ giữa các khoảng đồng biến,
nghịch biến của hàm số với dấu của f '(x).
Phương pháp giải:
a) Hàm số y = f(x) gọi là đồng biến (tăng) trên K nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1}\) < \({x_2}\) thì f(\({x_1}\)) < f(\({x_2}\)). Hàm số y = f(x) gọi là nghịch biến (giảm) trên K nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1}\) < \({x_2}\) thì f(\({x_1}\)) > f(\({x_2}\)).
b) Dựa vào công thức đạo hàm để tìm f '(x)
c) So sánh và rút ra nhận xét
Lời giải chi tiết:
a) Hàm số đồng biến trên khoảng (0; \( + \infty \))
Hàm số nghịch biến trên khoảng (\( - \infty \); 0)
b) f '(x) = (\({x^2}\))' = 2x
Ta có:
f '(x) > 0 \( \Leftrightarrow 2x > 0 \Leftrightarrow x > 0\)
f '(x) < 0 \( \Leftrightarrow 2x < 0 \Leftrightarrow x < 0\)
c) Nhận xét:
f’(x) > 0 trên K thì y = f(x) đồng biến trên K
f’(x) < 0 trên K thì y = f(x) nghịch biến trên K
TH2
Trả lời câu hỏi Thực hành 2 trang 9 SGK Toán 12 Chân trời sáng tạo
Xét tính đơn điệu của các hàm số sau:
a) \(f(x) = {x^3} - 6{x^2} + 9x\)
b) \(g(x) = \frac{1}{x}\)
Phương pháp giải:
Xác định tập xác định D, đạo hàm f’(x) và lập bảng biến thiên
Lời giải chi tiết:
a) \(f(x) = {x^3} - 6{x^2} + 9x\)
Tập xác định: \(D = \mathbb{R}\)
\(f'(x) = 3{x^2} - 12x + 9\)
\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Bảng biến thiên:
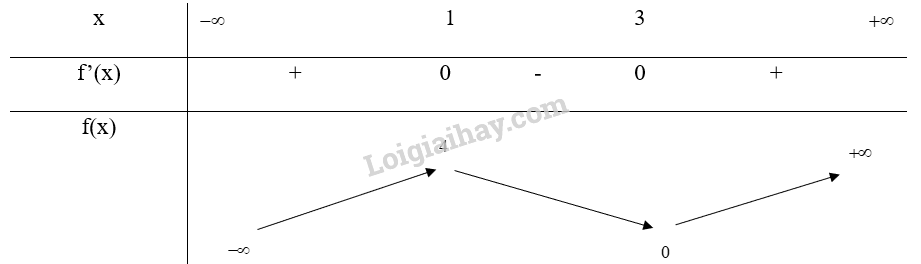
Vậy hàm số \(f(x) = {x^3} - 6{x^2} + 9x\) đồng biến trên các khoảng (\( - \infty \); 1) và (3; \( + \infty \)), nghịch biến trên khoảng (1; 3)
b) \(g(x) = \frac{1}{x}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 0\} \)
\(g'(x) = - \frac{1}{{{x^2}}}\)
Vì \({x^2} > 0\forall x \in \mathbb{R}\backslash \{ 0\} \) nên \(g'(x) < 0\forall x \in \mathbb{R}\backslash \{ 0\} \)
Bảng biến thiên:
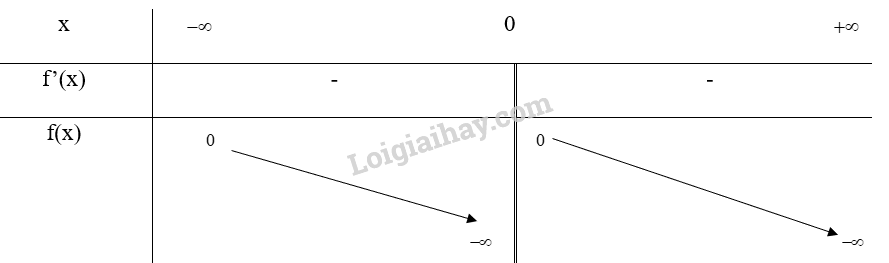
Vậy hàm số \(g(x) = \frac{1}{x}\) nghịch biến trên các khoảng (\( - \infty \); 0) và (0; \( + \infty \))
TH3
Trả lời câu hỏi Thực hành 3 trang 9 SGK Toán 12 Chân trời sáng tạo
Chứng minh rằng hàm số \(f\left( x \right) = 3x - sinx\) đồng biến trên \(\mathbb{R}\)
Phương pháp giải:
Tìm tập xác định D, đạo hàm f’(x) và dựa vào tính chất \( - 1 \le \cos x \le 1\)
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\)
\(f'(x) = 3 - \cos x\)
Ta có: \( - 1 \le \cos x \le 1\) nên \(2 \le 3 - \cos x \le 4\). Vì vậy \(f'(x) > 0\forall x \in \mathbb{R}\)
=> Hàm số \(f\left( x \right){\rm{ }} = {\rm{ }}3x{\rm{ }} - {\rm{ }}sinx\) đồng biến trên \(\mathbb{R}\)
VD1
Trả lời câu hỏi Vận dụng 1 trang 9 SGK Toán 12 Chân trời sáng tạo
Hãy trả lời câu hỏi trong Khởi động (trang 6) bằng cách xét dấu đạo hàm của hàm số \(h\left( t \right) = 6{t^3} - 81{t^2} + 324t\) với \(0 \le t \le 8\)
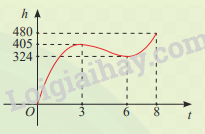
Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức \(h\left( t \right) = 6{t^3} - 81{t^2} + 324t\). Đồ thị của hàm số h(t) được biểu diễn trong hình bên. Trong các khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao? Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?
Phương pháp giải:
Xét dấu h’(x) để tìm ra các khoảng đồng biến, nghịch biến
Lời giải chi tiết:
\(h\left( t \right) = 6{t^3} - 81{t^2} + 324t\)
Tập xác định: \(D = \mathbb{R}\)
\(h'(t) = 18{t^2} - 162t + 324\)
\(h'(t) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = 6\end{array} \right.\)
Bảng biến thiên:

Trong thời gian từ lúc xuất phát đến thời điểm 3 phút, độ cao của khinh khí cầu tăng dần từ 0m lên 405m
Độ cao của khinh khí cầu tăng dần từ 0m lên 405m trong thời gian từ lúc xuất phát đến thời điểm 3 phút, từ 324m lên 480m trong thời gian từ 6 phút đến 8 phút
Độ cao của khinh khí cầu giảm dần từ 405m xuống 324m trong thời gian từ 3 phút đến 6 phút