Giải mục 1 trang 19,20 SGK Toán 12 tập 1 - Chân trời sáng tạo
Đường tiệm cận đứng
KP1
Trả lời câu hỏi Khám phá 1 trang 19 SGK Toán 12 Chân trời sáng tạo
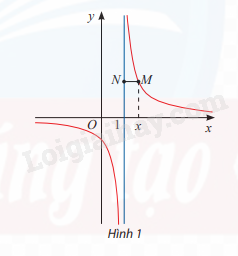
Cho hàm số \(y = \frac{1}{{x - 1}}\)có đồ thị như Hình 1.
a) Tìm \(\mathop {\lim }\limits_{x \to {1^ + }} = \frac{1}{{x - 1}},\mathop {\lim }\limits_{x \to {1^ - }} = \frac{1}{{x - 1}}\)
b) Gọi M là điểm trên đồ thị có hoành độ x. Đường thẳng đi qua M và vuông góc với trục Oy cắt đường thẳng x = 1 tại điểm N. Tính MN theo x và nhận xét về MN khi \(x \to {1^ + }\) và \(x \to {1^ - }\)
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Từ đồ thị ta thấy:
Khi x tiến dần tới 1 về bên phải thì y tiến dần đến \( + \infty \), vậy \(\mathop {\lim }\limits_{x \to {1^ + }} = \frac{1}{{x - 1}} = + \infty \)
Khi x tiến dần tới 1 về bên trái thì y tiến dần đến \( - \infty \), vậy \(\mathop {\lim }\limits_{x \to {1^ - }} = \frac{1}{{x - 1}} = - \infty \)
b) MN = x – 1
Khi \(x \to {1^ + }\) thì MN tiến dần về \( + \infty \) và khi \(x \to {1^ - }\) thì MN tiến dần về \( - \infty \)
TH1
Trả lời câu hỏi Thực hành 1 trang 20 SGK Toán 12 Chân trời sáng tạo
Tìm tiệm cận đứng của đồ thị các hàm số sau:
a) \(f(x) = \frac{{2x + 3}}{{ - x + 5}}\)
b) \(g(x) = \frac{{{x^2} - 2x}}{{x - 1}}\)
Phương pháp giải:
Đường thẳng x = a được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau thoả mãn:\(\mathop {\lim f(x) = }\limits_{x \to {a^ - }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ - }} - \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} - \infty \)
Lời giải chi tiết:
a) Xét \(f(x) = \frac{{2x + 3}}{{ - x + 5}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 5\} \)
Ta có: \(\mathop {\lim f(x) = }\limits_{x \to {5^ - }} \mathop {\lim }\limits_{x \to {5^ - }} \frac{{2x + 3}}{{ - x + 5}} = + \infty \), \(\mathop {\lim f(x) = }\limits_{x \to {5^ + }} \mathop {\lim }\limits_{x \to {5^ + }} \frac{{2x + 3}}{{ - x + 5}} = - \infty \)
Vậy đường thẳng x = 5 là một tiệm cận đứng của đồ thị hàm số
b) Xét \(g(x) = \frac{{{x^2} - 2x}}{{x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 1\} \)
Ta có: \(\mathop {\lim g(x) = }\limits_{x \to {1^ - }} \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 2x}}{{x - 1}} = + \infty \), \(\mathop {\lim g(x) = }\limits_{x \to {1^ + }} \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 2x}}{{x - 1}} = - \infty \)
Vậy đường thẳng x = 1 là một tiệm cận đứng của đồ thị hàm số