Giải mục 1 trang 26, 27 SGK Toán 12 tập 1 - Kết nối tri thức
Sơ đồ khảo sát hàm số
Đề bài
Trả lời câu hỏi Hoạt động 1 trang 26 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = {x^2} - 4x + 3\). Thực hiện lần lượt các yêu cầu sau:
a) Tính y’ và tìm các điểm tại đó \(y' = 0\).
b) Xét dấu y’ để tìm các khoảng đồng biến, khoảng nghịch biến và cực trị của hàm số.
c) Tính \(\mathop {\lim }\limits_{x \to - \infty } y\), \(\mathop {\lim }\limits_{x \to + \infty } y\) và lập bảng biến thiên của hàm số.
d) Vẽ đồ thị của hàm số và nhận xét về tính đối xứng của đồ thị.
Phương pháp giải - Xem chi tiết
a) Tính y’. Giải phương trình \(y' = 0\).
b) Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Sử dụng kiến thức về định lí cực trị hàm số để tìm cực trị hàm số: Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực tiểu của hàm số f(x).
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực đại của hàm số f(x).
d) Đồ thị hàm số bậc hai \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\) nhận đường thẳng \(x = \frac{{ - b}}{{2a}}\) làm trục đối xứng.
Lời giải chi tiết
a) Tập xác định: \(D = \mathbb{R}\)
Ta có: \(y' = 2x - 4,y' = 0 \Leftrightarrow 2x - 4 = 0 \Leftrightarrow x = 2\)
Vậy với \(x = 2\) thì \(y' = 0\).
b) Trên khoảng \(\left( { - \infty ;2} \right)\), \(y' < 0\) nên hàm số nghịch biến. Trên khoảng \(\left( {2; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến.
Hàm số đạt cực tiểu tại \(x = 2,\) giá trị cực tiểu \({y_{CT}} = - 1\). Hàm số không có cực đại.
c) \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^2} - 4x + 3} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {{x^2}\left( {1 - \frac{4}{x} + \frac{3}{{{x^2}}}} \right)} \right] = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^2} - 4x + 3} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {{x^2}\left( {1 - \frac{4}{x} + \frac{3}{{{x^2}}}} \right)} \right] = + \infty \)
Bảng biến thiên:
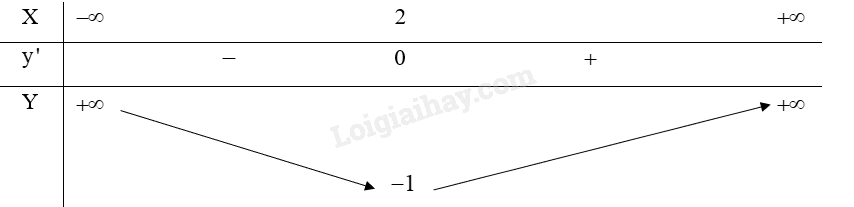
d) Đồ thị:
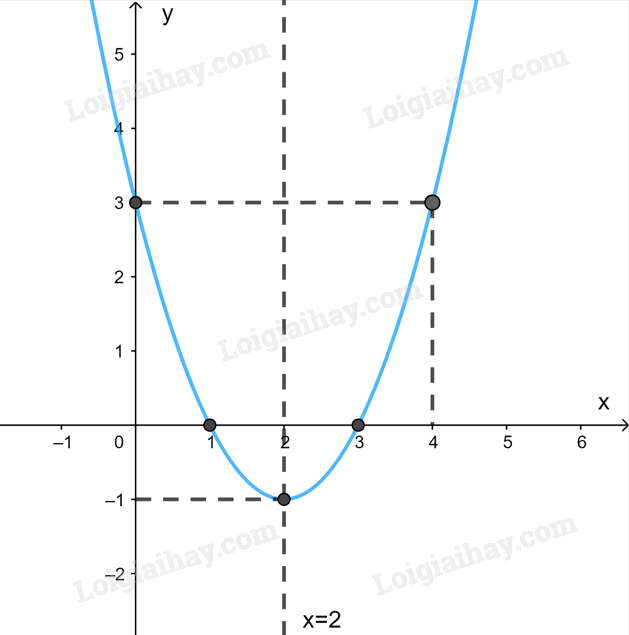
Giao điểm của đồ thị hàm số \(y = {x^2} - 4x + 3\) với trục tung là \(\left( {0;3} \right)\).
Ta có: \({x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\). Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm \(\left( {3;0} \right);\left( {1;0} \right)\).
Điểm \(\left( {4;3} \right)\) thuộc đồ thị hàm số \(y = {x^2} - 4x + 3\).
Đồ thị hàm số nhận đường thẳng \(x = 2\) làm trục đối xứng.
d) Đồ thị:
Giao điểm của đồ thị hàm số \(y = {x^2} - 4x + 3\) với trục tung là \(\left( {0;3} \right)\).
Ta có: \({x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\). Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm \(\left( {3;0} \right);\left( {1;0} \right)\).
Điểm \(\left( {4;3} \right)\) thuộc đồ thị hàm số \(y = {x^2} - 4x + 3\).
Đồ thị hàm số nhận đường thẳng \(x = 2\) làm trục đối xứng.