Giải mục 1 trang 12,13,14 SGK Toán 12 tập 2 - Kết nối tri thức — Không quảng cáo

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 13 SGK Toán 12 Kết nối tri thức

Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng \(y = x + 1\), trục hoành và hai đường thẳng \(x = 1,x = t\left( {1 \le t \le 4} \right)\) (H.4.3).

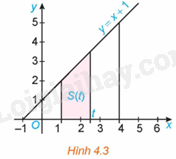
a) Tính diện tích S của T khi \(t = 4\).

b) Tính diện tích S(t) của T khi \(t \in \left[ {1;4} \right]\).

c) Chứng minh rằng S(t) là một nguyên hàm của hàm số \(f\left( t \right) = t + 1,t \in \left[ {1;4} \right]\) và diện tích \(S = S\left( 4 \right) - S\left( 1 \right)\).

Phương pháp giải:

Sử dụng kiến thức về diện tích hình thang để tính: Diện tích hình thang ABCD (AB//CD) là: \(S = \frac{{\left( {AB + CD} \right).h}}{2}\) với h là chiều cao của hình thang.

Lời giải chi tiết:

a) Gọi A, D lần lượt là giao điểm của các đường thẳng \(x = 1\), \(x = 4\) với trục hoành; B, C lần lượt là giao điểm của các đường thẳng \(x = 1\), \(x = 4\) với đường thẳng \(y = x + 1\).

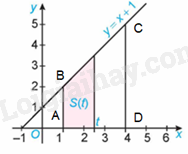
Khi đó, \(A\left( {1;0} \right),B\left( {1;2} \right),C\left( {4;5} \right),D\left( {4;0} \right)\). Do đó, \(AB = 2,CD = 5,AD = 3\)

Diện tích hình thang ABCD là: \(S = \frac{{\left( {AB + CD} \right).AD}}{2} = \frac{{\left( {2 + 5} \right).3}}{2} = \frac{{21}}{2}\)

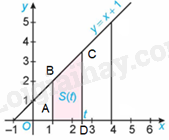
b) Gọi A, D lần lượt là giao điểm của các đường thẳng \(x = 1\), \(x = t\) với trục hoành, B, C lần lượt là giao điểm của đường thẳng \(x = 1\), \(x = t\) với đường thẳng \(y = x + 1\).

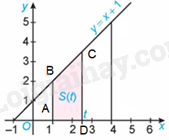
Khi đó, \(A\left( {1;0} \right),B\left( {1;2} \right),C\left( {t;t + 1} \right),D\left( {t;0} \right)\). Do đó, \(AB = 2,CD = t + 1,AD = t - 1\)

Diện tích hình thang ABCD là:

\(S\left( t \right) = \frac{{\left( {AB + CD} \right).AD}}{2} = \frac{{\left( {2 + t + 1} \right).\left( {t - 1} \right)}}{2} = \frac{{\left( {t + 3} \right)\left( {t - 1} \right)}}{2} = \frac{{{t^2} + 2t - 3}}{2}\)

c) Ta có: \(S'\left( t \right) = {\left( {\frac{{{t^2} + 2t - 3}}{2}} \right)'} = \frac{1}{2}\left( {2t + 2} \right) = t + 1 = f\left( t \right)\)

Do đó, S(t) là một nguyên hàm của hàm số \(f\left( t \right) = t + 1,t \in \left[ {1;4} \right]\).

Lại có: \(S\left( 4 \right) - S\left( 1 \right) = \frac{{{4^2} + 2.4 - 3}}{2} - \frac{{{1^2} + 2.1 - 3}}{2} = \frac{{21}}{2} - 0 = \frac{{21}}{2}\)

Suy ra: \(S = S\left( 4 \right) - S\left( 1 \right)\).

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 13 SGK Toán 12 Kết nối tri thức

Xét hình thang cong giới hạn bởi đồ thị \(y = {x^2}\), trục hoành và hai đường thẳng \(x = 1,x = 2\). Ta muốn tính diện tích S của hình thang cong này.

a) Với mỗi \(x \in \left[ {1;2} \right]\), gọi S(x) là diện tích phần hình thang cong đã cho nằm giữa hai đường thẳng vuông góc với trục Ox tại điểm có hoành độ bằng 1 và x (H.4.5).

Cho \(h > 0\) sao cho \(x + h < 2\). So sánh hiệu \(S\left( {x + h} \right) - S\left( x \right)\) với diện tích hai hình chữ nhật MNPQ và MNEF (H.4.6). Từ đó suy ra: \(0 \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 2xh + {h^2}\).

b) Cho \(h < 0\) sao cho \(x + h > 1\). Tương tự phần a, đánh giá hiệu \(S\left( x \right) - S\left( {x + h} \right)\) và từ đó suy ra \(2xh + {h^2} \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 0\).

c) Từ kết quả phần a và phần b, suy ra với mọi \(h \ne 0\), ta có

\(\left| {\frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2}} \right| \le 2x\left| h \right| + {h^2}\).

Từ đó chứng minh \(S'\left( x \right) = {x^2},x \in \left( {1;2} \right)\). Người ta chứng minh được \(S'\left( 1 \right) = 1,S'\left( 2 \right) = 4\), tức là S(x) là một nguyên hàm của \({x^2}\) trên \(\left[ {1;2} \right]\).

d) Từ kết quả của phần c, ta có \(S\left( x \right) = \frac{{{x^3}}}{3} + C\). Sử dụng điều này với lưu ý \(S\left( 1 \right) = 0\) và diện tích cần tính \(S = S\left( 2 \right)\), hãy tính S.

Gọi F(x) là một nguyên hàm tùy ý của \(f\left( x \right) = {x^2}\) trên \(\left[ {1;2} \right]\). Hãy so sánh S và \(F\left( 2 \right) - F\left( 1 \right)\).

Phương pháp giải:

Sử dụng kiến thức về hình thang cong để tính: Hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\), trong đó f(x) là hàm liên tục không âm trên đoạn [a; b] gọi là một hình thang cong.

Lời giải chi tiết:

a) Với \(h > 0\) sao cho \(x + h < 2\), gọi \({S_{MNPQ}}\) và \({S_{MNEF}}\) lần lượt là diện tích các hình chữ nhật MNPQ và MNEF thì \({S_{MNPQ}} \le S\left( {x + h} \right) - S\left( x \right) \le {S_{MNEF}}\)

Diện tích hình chữ nhật MNPQ là: \({S_{MNPQ}} = MN.MQ = \left( {x + h - x} \right){x^2} = h{x^2}\)

Diện tích hình chữ nhật MNEF là: \({S_{MNEF}} = MN.NE = \left( {x + h - x} \right){\left( {x + h} \right)^2} = h{\left( {x + h} \right)^2}\)

Do đó, \(h{x^2} \le S\left( {x + h} \right) - S\left( x \right) \le h{\left( {x + h} \right)^2}\). Vậy \(0 \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 2xh + {h^2}\)

b)

Với \(h < 0\) sao cho \(x + h > 1\), gọi \({S_{MNPQ}}\) và \({S_{MNEF}}\) lần lượt là diện tích các hình chữ nhật MNPQ và MNEF thì \({S_{MNPQ}} \le S\left( x \right) - S\left( {x + h} \right) \le {S_{MNEF}}\)

Diện tích hình chữ nhật MNPQ là: \({S_{MNPQ}} = MN.MQ =  - h{\left( {x + h} \right)^2} > 0\)

Diện tích hình chữ nhật MNEF là: \({S_{MNEF}} = MN.NE =  - h{x^2}\)

Do đó, \( - h{\left( {x + h} \right)^2} \le S\left( {x + h} \right) - S\left( x \right) \le  - h{x^2}\)

Vậy \(2xh + {h^2} \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 0\)  (do \(h < 0\) nên \( - h > 0\))

c) Từ phần a và phần b, suy ra với mọi \(h \ne 0\), ta có: \(\left| {\frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2}} \right| \le 2x\left| h \right| + {h^2}\)

Do đó, \(S'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} = {x^2},x \in \left( {1;2} \right)\). Suy ra, \(S'\left( 1 \right) = 1,S'\left( 2 \right) = 4\).

Do đó, S(x) là một nguyên hàm của \({x^2}\) trên \(\left[ {1;2} \right]\).

d) Theo c ta có: \(S\left( x \right) = \frac{{{x^3}}}{3} + C\), \(S\left( 1 \right) = 0\)  nên \(\frac{1}{3} + C = 0 \Leftrightarrow C = \frac{{ - 1}}{3}\).

Do đó, \(S\left( x \right) = \frac{{{x^3}}}{3} - \frac{1}{3}\)

Diện tích cần tính là: \(S = S\left( 2 \right) = \frac{{{2^3}}}{3} - \frac{1}{3} = \frac{7}{3}\)

Vì F(x) là một nguyên hàm tùy ý của \(f\left( x \right) = {x^2}\) trên \(\left[ {1;2} \right]\) nên \(F\left( x \right) = \frac{{{x^3}}}{3} + C,C \in \mathbb{R}\)

Ta có: \(F\left( 2 \right) - F\left( 1 \right) = \frac{7}{3} - 0 = \frac{7}{3} = S\). Do đó, \(S = F\left( 2 \right) - F\left( 1 \right)\)

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 14 SGK Toán 12 Kết nối tri thức

Giả sử f(x) là hàm số liên tục trên đoạn \(\left[ {a;b} \right]\), F(x) và G(x) là hai nguyên hàm tùy ý của f(x) trên đoạn \(\left[ {a;b} \right]\). Chứng minh rằng \(F\left( b \right) - F\left( a \right) = G\left( b \right) - G\left( a \right)\).

Phương pháp giải:

Sử dụng kiến thức về họ nguyên hàm của một hàm số để chứng minh: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.

Lời giải chi tiết:

Vì F(x) và G(x) là hai nguyên hàm tùy ý của f(x) trên đoạn \(\left[ {a;b} \right]\) nên tồn tại hằng số C sao cho \(F\left( x \right) = G\left( x \right) + C\).

Do đó, \(F\left( b \right) - F\left( a \right) = G\left( b \right) + C - G\left( a \right) - C = G\left( b \right) - G\left( a \right)\)

LT1

Trả lời câu hỏi Luyện tập 1 trang 15 SGK Toán 12 Kết nối tri thức

Tính:

a) \(\int\limits_0^1 {{e^x}dx} \);

b) \(\int\limits_1^e {\frac{1}{x}dx} \);

c) \(\int\limits_0^{\frac{\pi }{2}} {\sin xdx} \);

d) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{3}} {\frac{{dx}}{{{{\sin }^2}x}}} \).

Phương pháp giải:

Sử dụng kiến thức về định nghĩa tích phân để tính: Cho f(x) là hàm số liên tục trên đoạn [a; b]. Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a; b] thì hiệu số \(F\left( b \right) - F\left( a \right)\) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu \(\int\limits_a^b {f\left( x \right)dx} \).

Lời giải chi tiết:

a) \(\int\limits_0^1 {{e^x}dx}  = {e^x}\left| \begin{array}{l}1\\0\end{array} \right. = {e^1} - {e^0} = e - 1\);

b) \(\int\limits_1^e {\frac{1}{x}dx}  = \ln \left| x \right|\left| \begin{array}{l}e\\1\end{array} \right. = \ln e - \ln 1 = 1\);

c) \(\int\limits_0^{\frac{\pi }{2}} {\sin xdx}  =  - \cos x\left| \begin{array}{l}\frac{\pi }{2}\\0\end{array} \right. =  - \cos \frac{\pi }{2} + \cos 0 = 1\);

d) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{3}} {\frac{{dx}}{{{{\sin }^2}x}}}  =  - \tan x\left| \begin{array}{l}\frac{\pi }{3}\\\frac{\pi }{6}\end{array} \right. =  - \cot \frac{\pi }{3} + \cot \frac{\pi }{6} =  - \frac{{\sqrt 3 }}{3} + \sqrt 3  = \frac{{2\sqrt 3 }}{3}\).

LT2

Trả lời câu hỏi Luyện tập 2 trang 16 SGK Toán 12 Kết nối tri thức

Sử dụng ý nghĩa hình học của tích phân, tính:

a) \(\int\limits_1^3 {\left( {2x + 1} \right)dx} \);

b) \(\int\limits_{ - 2}^2 {\sqrt {4 - {x^2}} dx} \).

Phương pháp giải:

Sử dụng kiến thức về ý nghĩa hình học của tích phân để tính: Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b], thì tích phân \(\int\limits_a^b {f\left( x \right)dx} \) là diện tích S của hình thang cong giới hạn bởi đồ thị \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\). Vậy \(S = \int\limits_a^b {f\left( x \right)dx} \).

Lời giải chi tiết:

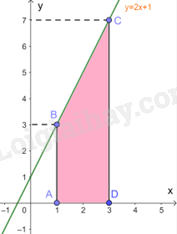
a) Tích phân cần tính là diện tích của hình thang vuông ABCD, có đáy nhỏ \(AB = 3,\) đáy lớn \(CD = 7\) và đường cao \(AD = 2\).

Do đó, \(\int\limits_1^3 {\left( {2x + 1} \right)dx}  = {S_{ABCD}} = \frac{1}{2}\left( {AB + CD} \right)AD = \frac{1}{2}\left( {3 + 7} \right).2 = 10\)

b) Ta có \(y = \sqrt {4 - {x^2}} \) là phương trình nửa phía trên trục hoành của đường tròn tâm tại gốc tọa độ O và bán kính 2. Do đó, tích phân cần tính là diện tích nửa phía trên trục hoành của hình tròn tương ứng.

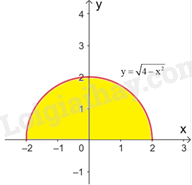
Vậy \(\int\limits_{ - 2}^2 {\sqrt {4 - {x^2}} dx}  = 2\pi \)

VD1

Trả lời câu hỏi Vận dụng 1 trang 16 SGK Toán 12 Kết nối tri thức

Giải quyết bài toán ở tình huống mở đầu .

Phương pháp giải:

Sử dụng kiến thức về định nghĩa tích phân để tính: Cho f(x) là hàm số liên tục trên đoạn [a; b]. Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a; b] thì hiệu số \(F\left( b \right) - F\left( a \right)\) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu \(\int\limits_a^b {f\left( x \right)dx} \)

Sử dụng kiến thức về quan hệ giữa hàm số vận tốc và hàm số quãng đường để tính: Hàm số quãng đường S(t) là một nguyên hàm của hàm số vận tốc v(t).

Lời giải chi tiết:

Lấy mốc thời gian là lúc ô tô bắt đầu được phanh. Gọi T là thời điểm ô tô dừng.

Xe dừng hẳn khi \(v\left( T \right) = 0.\) Do đó, \(0 =  - 40T + 20\) nên \(T = \frac{1}{2}\). Như vậy, khoảng thời gian từ lúc đạp phanh đến khi dừng hẳn của ô tô là 0,5 giây.

Vì \(v\left( t \right) = S'\left( t \right)\) nên S(t) là một nguyên hàm của hàm vận tốc v(t).

Từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được số mét là:

Do đó, \(S\left( t \right) = \int\limits_0^{\frac{1}{2}} {v\left( t \right)dt}  = \int\limits_0^{\frac{1}{2}} {\left( { - 40t + 20} \right)dt = \left( { - 20{t^2} + 20t} \right)\left| \begin{array}{l}\frac{1}{2}\\0\end{array} \right. = }  - 20.{\left( {\frac{1}{2}} \right)^2} + 20.\frac{1}{2} = 5\left( m \right)\)

Vậy từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được 5m.