Giải mục 1 trang 19,20,21 SGK Toán 12 tập 2 - Kết nối tri thức — Không quảng cáo

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 19 SGK Toán 12 Kết nối tri thức

Xét hình phẳng giới hạn bởi đồ thị $y = f\left( x \right) = x + 1$, trục hoành và hai đường thẳng $x =  - 2,x = 1$ (H.4.12).

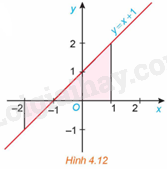
a) Tính diện tích S của hình phẳng này.

b) Tính $\int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|dx}$ và so sánh với S.

Phương pháp giải:

Sử dụng kiến thức về tính chất của tích phân để tính: Cho f(x), g(x) là các hàm số liên tục trên đoạn [a; b]. Khi đó, ta có: $\int\limits_a^b {f\left( x \right)dx}  = \int\limits_a^c {f\left( x \right)dx}  + \int\limits_c^b {f\left( x \right)dx}$ $\left( {a < c < b} \right)$.

Lời giải chi tiết:

a) Đặt tên các điểm như hình vẽ. Khi đó, $AD = 1,DE = 1,AC = 2,CB = 2$

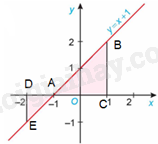
Diện tích S của hình phẳng là:

$S = {S_{\Delta EAD}} + {S_{\Delta ABC}} = \frac{1}{2}AD.DE + \frac{1}{2}AC.BC = \frac{1}{2}.1.1 + \frac{1}{2}.2.2 = \frac{1}{2} + 2 = \frac{5}{2}$

b) $\int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|dx}  = \int\limits_{ - 2}^1 {\left| {x + 1} \right|dx}  = \int\limits_{ - 2}^{ - 1} {\left| {x + 1} \right|dx}  + \int\limits_{ - 1}^1 {\left| {x + 1} \right|dx =  - \int\limits_{ - 2}^{ - 1} {\left( {x + 1} \right)dx}  + \int\limits_{ - 1}^1 {\left( {x + 1} \right)dx} }$

$=  - \left( {\frac{{{x^2}}}{2} + x} \right)\left| \begin{array}{l} - 1\\ - 2\end{array} \right. + \left( {\frac{{{x^2}}}{2} + x} \right)\left| \begin{array}{l}1\\ - 1\end{array} \right. = \left( {\frac{1}{2} + 1 - \frac{1}{2} + 1} \right) - \left( {\frac{{{1^2}}}{2} - 1 - \frac{{{{\left( { - 2} \right)}^2}}}{2} + 2} \right) = 2 + \frac{1}{2} = \frac{5}{2}$

LT1

Trả lời câu hỏi Luyện tập 1 trang 20 SGK Toán 12 Kết nối tri thức

Tính diện tích hình phẳng giới hạn bởi parabol $y = {x^2} - 4$, trục hoành và hai đường thẳng $x = 0,x = 3$ (H.4.15).

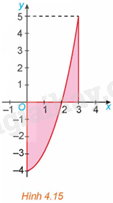
Phương pháp giải:

Sử dụng kiến thức về ứng dụng tích phân để tính diện tích hình phẳng để tính: Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số f(x) liên tục, trục hoành và hai đường thẳng $x = a,x = b\left( {a < b} \right)$, được tính bằng công thức $S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx}$.

Lời giải chi tiết:

Diện tích hình phẳng cần tính là:

$S = \int\limits_0^3 {\left| {{x^2} - 4} \right|dx}  = \int\limits_0^2 {\left| {{x^2} - 4} \right|dx}  + \int\limits_2^3 {\left| {{x^2} - 4} \right|dx}  =  - \int\limits_0^2 {\left( {{x^2} - 4} \right)dx}  + \int\limits_2^3 {\left( {{x^2} - 4} \right)dx}$

$=  - \left( {\frac{{{x^3}}}{3} - 4x} \right)\left| \begin{array}{l}2\\0\end{array} \right. + \left( {\frac{{{x^3}}}{3} - 4x} \right)\left| \begin{array}{l}3\\2\end{array} \right. =  - \left( {\frac{{{2^3}}}{3} - 4.2} \right) + \left( {\frac{{{3^3}}}{3} - 4.3 - \frac{{{2^3}}}{3} + 4.2} \right) = \frac{{16}}{3} + \frac{7}{3} = \frac{{23}}{3}$

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 20 SGK Toán 12 Kết nối tri thức

Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $f\left( x \right) =  - {x^2} + 4x,$ $g\left( x \right) = x$ và hai đường thẳng $x = 1,x = 3$ (H.4.16)

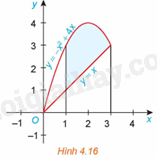
a) Giả sử ${S_1}$ là diện tích hình phẳng giới hạn bởi parabol $y =  - {x^2} + 4x$, trục hoành và hai đường thẳng $x = 1,x = 3$; ${S_2}$ là diện tích hình phẳng giới hạn bởi đường thẳng $y = x$, trục hoành và hai đường thẳng $x = 1,x = 3$. Tính ${S_1}$, ${S_2}$ và từ đó suy ra S.

b) Tính $\int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx}$ và so sánh với S.

Phương pháp giải:

Sử dụng kiến thức về ứng dụng tích phân để tính diện tích hình phẳng để tính: Diện tích S của hàm số f(x) liên tục, trục hoành và hai đường thẳng $x = a,x = b\left( {a < b} \right)$, được tính bằng công thức $S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx}$.

Lời giải chi tiết:

a) Diện tích hình phẳng giới hạn bởi parabol $y =  - {x^2} + 4x$, trục hoành và hai đường thẳng $x = 1,x = 3$ là:

${S_1} = \int\limits_1^3 {\left| { - {x^2} + 4x} \right|dx}  = \int\limits_1^3 {\left( { - {x^2} + 4x} \right)dx}  = \left( {\frac{{ - {x^3}}}{3} + 2{x^2}} \right)\left| \begin{array}{l}3\\1\end{array} \right. = \frac{{ - {3^3}}}{3} + {2.3^2} + \frac{1}{3} - {2.1^2} = \frac{{22}}{3}$

Diện tích hình phẳng giới hạn bởi parabol $y = x$, trục hoành và hai đường thẳng $x = 1,x = 3$ là: ${S_2} = \int\limits_1^3 {\left| x \right|dx}  = \int\limits_1^3 {xdx}  = \frac{{{x^2}}}{2}\left| \begin{array}{l}3\\1\end{array} \right. = \frac{{{3^2}}}{2} - \frac{1}{2} = 4$

Do đó, $S = {S_1} - {S_2} = \frac{{22}}{3} - 4 = \frac{{10}}{3}$

b) $\int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx}  = \int\limits_1^3 {\left| { - {x^2} + 3x} \right|dx}  = \int\limits_1^3 {\left( { - {x^2} + 3x} \right)dx}  = \left( {\frac{{ - {x^3}}}{3} + \frac{{3{x^2}}}{2}} \right)\left| \begin{array}{l}3\\1\end{array} \right.$

$= \frac{{ - {3^3}}}{3} + \frac{{{{3.3}^2}}}{2} + \frac{1}{3} - \frac{3}{2} = \frac{{10}}{3}$

Do đó, $S = \int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx}$

LT2

Trả lời câu hỏi Luyện tập 2 trang 21 SGK Toán 12 Kết nối tri thức

Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $y = \sqrt x ,y = x - 2$ và hai đường thẳng $x = 1,x = 4$.

Phương pháp giải:

Sử dụng kiến thức về diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và đường thẳng $x = a,x = b$ để tính: Diện tích S của hình phẳng giới hạn đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng $x = a,x = b$, được tính bằng công thức $S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx}$.

Lời giải chi tiết:

Diện tích hình phẳng cần tính là:

$\int\limits_1^4 {\left| {x - \sqrt x  - 2} \right|dx}  =  - \int\limits_1^4 {\left( {x - \sqrt x  - 2} \right)dx}  =  - \left( {\frac{{{x^2}}}{2} - \frac{{2x\sqrt x }}{3} - 2x} \right)\left| \begin{array}{l}4\\1\end{array} \right.$

$=  - \left( {\frac{{{4^2}}}{2} - \frac{{2.4\sqrt 4 }}{3} - 2.4 - \frac{1}{2} + \frac{{2.1.\sqrt 1 }}{3} + 2.1} \right) = \frac{{19}}{6}$

VD1

Trả lời câu hỏi Vận dụng 1 trang 22 SGK Toán 12 Kết nối tri thức

Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau $\left( {{x_o};{p_o}} \right)$ của đồ thị hàm cầu $p = D\left( x \right)$ và đồ thị hàm cung $p = S\left( x \right)$ được gọi là điểm cân bằng .

Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang $p = {p_o}$ và đường thẳng đứng $x = 0$ là thặng dư tiêu dùng . Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang $p = {p_o}$ và đường thẳng đứng $x = 0$ được gọi là thặng dư sản xuất , như trong Hình 4.19.

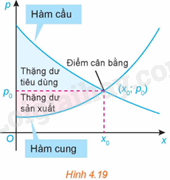
(Theo R. Larson, Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009 )

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: $p =  - 0,36x + 9$ và hàm cung: $p = 0,14x + 2$, trong đó x là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.

Phương pháp giải:

Sử dụng kiến thức về diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và đường thẳng $x = a,x = b$ để tính: Diện tích S của hình phẳng giới hạn đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng $x = a,x = b$, được tính bằng công thức $S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx}$.

Lời giải chi tiết:

Gọi điểm M là giao điểm của hàm cầu $p =  - 0,36x + 9$ và hàm cung $p = 0,14x + 2$

Khi đó, phương trình hoành độ giao điểm của hàm cầu và hàm cung là:

$- 0,36x + 9 = 0,14x + 2$, suy ra $x = 14$ nên $p =  - 0,36.14 + 9 = \frac{{99}}{{25}}$. Do đó, $M\left( {14;\frac{{99}}{{25}}} \right)$

Đồ thị hàm số $p =  - 0,36x + 9$ đi qua điểm $M\left( {14;\frac{{99}}{{25}}} \right)$ và điểm N(0 ;9)

Đồ thị hàm số $p = 0,14x + 2$ đi qua điểm $M\left( {14;\frac{{99}}{{25}}} \right)$ và điểm P(0; 2)

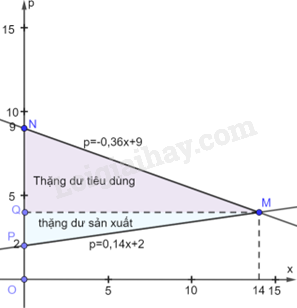
Diện tích hình giới hạn bởi đồ thị hàm số $p =  - 0,36x + 9$, trục hoành và hai đường thẳng $x = 0,x = 14$ là: ${S_1} = \int\limits_0^{14} {\left| { - 0,36x + 9} \right|dx}  = \int\limits_0^{14} {\left( { - 0,36x + 9} \right)dx}  = \left( { - 0,18{x^2} + 9x} \right)\left| \begin{array}{l}14\\0\end{array} \right.$

$=  - 0,{18.14^2} + 9.14 = 90,72$

Diện tích hình giới hạn bởi đồ thị hàm số $p = 0,14x + 2$, trục hoành và hai đường thẳng $x = 0,x = 14$ là:

${S_2} = \int\limits_0^{14} {\left| {0,14x + 2} \right|dx}  = \int\limits_0^{14} {\left( {0,14x + 2} \right)dx}  = \left( {0,07{x^2} + 2x} \right)\left| \begin{array}{l}14\\0\end{array} \right.$$= 0,{07.14^2} + 2.14 = 41,72$

Thặng dư tiêu dùng cho sản phẩm này là: ${S_1} - OQ.QM = 90,72 - 14.\frac{{99}}{{25}} = 35,28$

Thặng dư sản xuất cho sản phẩm này là: $OQ.OM - {S_2} = 14.\frac{{99}}{{25}} - 41,72 = 13,72$