Giải mục 1 trang 20, 21 SGK Toán 12 tập 1 - Kết nối tri thức — Không quảng cáo

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 20 SGK Toán 12 Kết nối tri thức

Cho hàm số $y = f\left( x \right) = \frac{{2x + 1}}{x}$ có đồ thị (C). Với $x > 0$, xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng $y = 2$ (H.1.19).

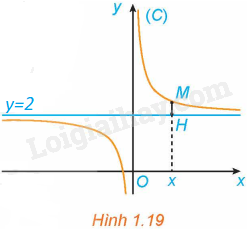
a) Tính khoảng cách MH.

b) Có nhận xét gì về khoảng cách MH khi $x \to  + \infty$?

Phương pháp giải:

Sử dụng kiến thức về giới hạn của hàm số để tính.

Lời giải chi tiết:

a) Ta có: $M\left( {x;\frac{{2x + 1}}{x}} \right)$; $H\left( {x;2} \right)$.

Do đó, $MH = \sqrt {{{\left( {x - x} \right)}^2} + {{\left( {2 - \frac{{2x + 1}}{x}} \right)}^2}}  = \sqrt {{{\left( {\frac{{2x - 2x - 1}}{x}} \right)}^2}}  = \frac{1}{x}$ (do $x > 0$)

b) Ta có: $\mathop {\lim }\limits_{x \to  + \infty } \frac{1}{x} = 0$. Do đó, khi $x \to  + \infty$ thì $MH \to 0$.

LT1

Trả lời câu hỏi Luyện tập 1 trang 21 SGK Toán 12 Kết nối tri thức

Tìm tiệm cận ngang của đồ thị hàm số $y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}$.

Phương pháp giải:

Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng $y = {y_0}$ gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số $y = f\left( x \right)$ nếu $\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = {y_0}$ hoặc $\mathop {\lim }\limits_{x \to  - \infty } f\left( x \right) = {y_0}$.

Lời giải chi tiết:

Ta có: $\mathop {\lim }\limits_{x \to  + \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2;\mathop {\lim }\limits_{x \to  - \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to  - \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2$.

Do đó, tiệm cận ngang của đồ thị hàm số $y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}$ là $y = 2$.

VD1

Trả lời câu hỏi Vận dụng 1 trang 21 SGK Toán 12 Kết nối tri thức

Giải bài toán trong tình huống mở đầu.

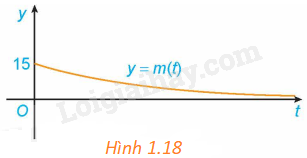
Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số $m\left( t \right) = 15{e^{ - 0,012t}}$. Khối lượng m(t) thay đổi ra sao khi $t \to  + \infty$? Điều này thể hiện trên Hình 1.18 như thế nào?

Phương pháp giải:

Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng $y = {y_0}$ gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số $y = f\left( x \right)$ nếu $\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = {y_0}$ hoặc $\mathop {\lim }\limits_{x \to  - \infty } f\left( x \right) = {y_0}$.

Lời giải chi tiết:

Ta có: $\mathop {\lim }\limits_{t \to  + \infty } m\left( t \right) = \mathop {\lim }\limits_{t \to  + \infty } 15{e^{ - 0,012t}} = \mathop {\lim }\limits_{t \to  + \infty } \frac{{15}}{{{e^{0,012t}}}} = 0$

Do đó, $m\left( t \right) \to 0$ khi $t \to  + \infty$.

Trong hình 1.18, khi $t \to  + \infty$ thì m(t) càng gần trục hoành Ot (nhưng không chạm trục Ot).