Giải mục 1 trang 6, 7 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
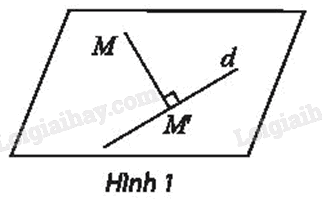
Trong mặt phẳng, cho đường thẳng d và điểm M. Gọi M’ là hình chiếu vuông góc của M trên đường thẳng d.
Khám phá 1
Trong mặt phẳng, cho đường thẳng d và điểm M. Gọi M’ là hình chiếu vuông góc của M trên đường thẳng d.
Vẽ ba điểm A, B, C tùy ý và tìm hình chiếu vuông góc A’, B’, C’ của chúng trên d.
Phương pháp giải:
Để tìm hình chiếu của một điểm A lên một đường thẳng d. Từ điểm A hạ đường thẳng AH vuông góc với d tại H. Khi đó, H là hình chiếu vuông góc của A lên d.
Lời giải chi tiết:
Giả sử chọn ba điểm A, B, C như hình vẽ dưới đây. Khi đó hình chiếu vuông góc A’, B’, C’ của chúng trên d được biểu diễn như hình vẽ dưới đây:
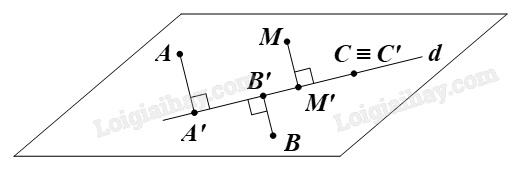
Thực hành 1
Trong mặt phẳng tọa độ Oxy, ứng mỗi điểm M(x; y) quy tắc f xác định điểm M’(–3x; 3y). Hãy cho biết f có phải là phép biến hình không. Nếu có, tìm ảnh của điểm A(–1; 2) qua f.
Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
+ Theo đề, ta có f(M) = M’, với tọa độ M(x; y), M’(–3x; 3y).
Ta thấy f là một quy tắc sao cho: ứng với mỗi điểm M đều xác định duy nhất một điểm M’.
Vậy f là một phép biến hình.
+ Gọi A’ là ảnh của điểm A(–1; 2) qua phép biến hình f.
Ta có x A’ = –3x A = –3.(–1) = 3 và y A’ = 3y A = 3.2 = 6.
Vậy ảnh của điểm A(–1; 2) qua phép biến hình f là điểm A’(3; 6).