Giải mục 1 trang 25, 26, 27 Chuyên đề học tập Toán 11 - Chân trời sáng tạo

Tìm phép biến hình biến \(\Delta \)BAC thành \(\Delta \)BA’C’ (Hình 1).

Khám phá 1

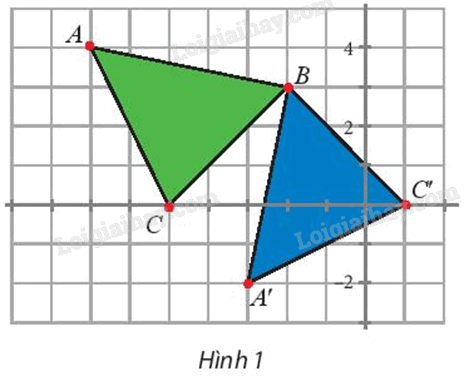
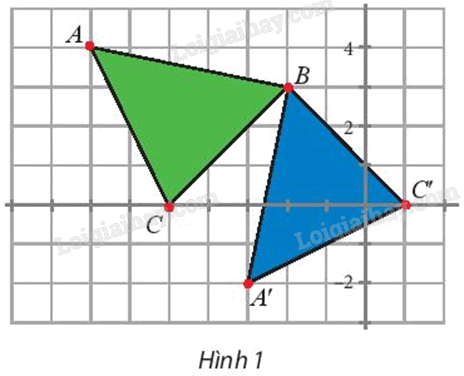
a) Tìm phép biến hình biến \(\Delta \)BAC thành \(\Delta \)BA’C’ (Hình 1).

b) Trong mặt phẳng, cho điểm O cố định (Hình 2).

Gọi f là quy tắc ứng với mỗi điểm M trùng O cho ta điểm O và ứng với điểm M khác O cho ta một điểm M’ xác định như sau:

– Dùng compa vẽ đường tròn (C) tâm O bán kính OM.

– Trên (C) chọn điểm M’ sao cho góc lượng giác (OM, OM’) bằng 60°.

Quy tắc f có phải là một phép biến hình không?

Hãy vẽ điểm M’ theo quy tắc trên nếu thay góc 60° bởi góc –30°.

Phương pháp giải:

Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).

Lời giải chi tiết:

a) Để tìm phép biến hình biến ∆BAC thành ∆BA’C’, ta tìm phép biến hình biến điểm B thành chính nó, biến điểm A thành điểm A’, biến điểm C thành điểm C’.

Với \(\;A\left( {-7;{\rm{ }}4} \right),{\rm{ }}B\left( {-2;{\rm{ }}3} \right),{\rm{ }}C\left( {-5;{\rm{ }}0} \right),{\rm{ }}A'\left( {-3;{\rm{ }}-2} \right),{\rm{ }}C'\left( {1;{\rm{ }}0} \right),\) ta có:

\(\overrightarrow {BA} = \left( { - 5;1} \right),\overrightarrow {BA'} = \left( { - 1; - 5} \right),\overrightarrow {AA'} = \left( {4; - 6} \right)\)

Suy ra \(BA = BA' = \sqrt {26} ;\,AA' = 2\sqrt {13} \)

Khi đó \(\cos \widehat {ABA'} = \frac{{B{A^2} + BA{'^2} - AA{'^2}}}{{2.BA.BA'}} = \frac{{26 + 26 - {{\left( {2\sqrt {13} } \right)}^2}}}{{2.\sqrt {26} .\sqrt {26} }} = 0\)

Vì vậy \(\left( {BA,BA'} \right) = \widehat {ABA'} = 90^\circ \)

Suy ra phép biến hình biến đoạn thẳng BA thành đoạn thẳng BA’ là phép biến hình biến điểm B thành điểm B, biến điểm A thành điểm A’ sao cho BA’ = BA và góc lượng giác \(\left( {BA,{\rm{ }}BA'} \right){\rm{ }} = {\rm{ }}90^\circ {\rm{ }}\left( 1 \right)\)

Thực hiện tương tự, ta được \(BC = BC' = 3\sqrt 2 ;\,\left( {BC,B{C'}} \right) = 90^\circ \)

Suy ra phép biến hình biến đoạn thẳng BC thành đoạn thẳng BC’ là phép biến hình biến điểm B thành điểm B, biến điểm C thành điểm C’ sao cho BC’ = BC và góc lượng giác \(\left( {BC,{\rm{ }}BC'} \right){\rm{ }} = {\rm{ }}90^\circ {\rm{ }}\left( 2 \right)\)

Từ (1), (2), ta thu được phép biến hình biến ∆BAC thành ∆BA’C’ là phép biến hình biến điểm B thành chính nó, biến điểm A thành điểm A’ sao cho và góc lượng giác \(\left( {BA,{\rm{ }}BA'} \right){\rm{ }} = {\rm{ }}90^\circ \) và biến điểm C thành điểm C’ sao cho \(BC'{\rm{ }} = {\rm{ }}BC\) và góc lượng giác \(\left( {BC,{\rm{ }}BC'} \right){\rm{ }} = {\rm{ }}90^\circ .\)

b) Đặt \({\rm{ }}f\left( M \right){\rm{ }} = {\rm{ }}M'.\) Trong đó, M’ là điểm nằm trên (C) sao cho góc lượng giác \(\left( {OM,{\rm{ }}OM'} \right)\) bằng 60°.

Ta thấy f là một quy tắc sao cho ứng với mỗi điểm M đều xác định duy nhất một điểm M’.

Vậy f là một phép biến hình.

Cách vẽ điểm M’ theo quy tắc trên với góc lượng giác (OM, OM’) bằng –30°:

– Dùng compa vẽ đường tròn (C) tâm O bán kính OM.

– Trên (C) chọn điểm M’ sao cho góc lượng giác (OM, OM’) bằng –30°.

Ta có hình vẽ sau:

Thực hành 1

Trong mặt phẳng tọa độ Oxy, tìm tọa độ của các điểm là ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) lần lượt qua các phép quay \({Q_{\left( {O,{\rm{ }}45^\circ } \right)}},{\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}},{\rm{ }}{Q_{\left( {O,{\rm{ }}180^\circ } \right)}},{\rm{ }}{Q_{\left( {O,{\rm{ }}360^\circ } \right)}}.\)

Phương pháp giải:

Phép quay tâm O, góc quay :

Khi đó, \(\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)

Lời giải chi tiết:

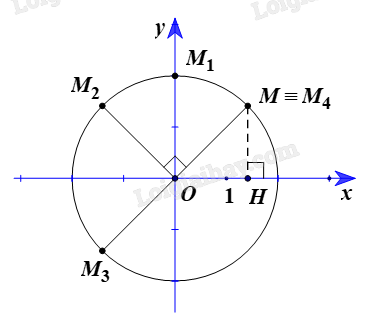
Ta có \(\overrightarrow {OM} = \left( {\sqrt 2 ;\sqrt 2 } \right)\). Suy ra OM = 2.

Vẽ đường tròn (C) tâm O bán kính OM.

⦁ Ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) qua phép quay \({Q_{\left( {O,{\rm{ }}45^\circ } \right)}}\)

Ta có \({Q_{\left( {O,{\rm{ }}45^\circ } \right)}}\) biến điểm M khác O thành điểm M ₁ sao cho \(O{M_1}\; = {\rm{ }}OM{\rm{ }} = {\rm{ }}2\)và \((OM,{\rm{ }}O{M_1}){\rm{ }} = {\rm{ }}45^\circ \) nên \(\widehat {MO{M_1}} = 45^\circ \)

Kẻ \(MH \bot Ox\) tại H.

Tam giác OMH vuông tại H: \(\cos \widehat {MOH} = \frac{{OH}}{{OM}} = \frac{{\sqrt 2 }}{2}\)

Suy ra \(\widehat {MOH} = 45^\circ \)

Ta có \(\widehat {HO{M_1}} = \widehat {HOM} + \widehat {MO{M_1}} = 45^\circ + 45^\circ = 90^\circ \)

Suy ra \({M_1}\; \in {\rm{ }}Oy\) nên \({x_{{M_1}}} = 0\)

Mà \(O{M_1}\; = {\rm{ }}2\) (chứng minh trên) nên tọa độ \({M_1}\left( {0;{\rm{ }}2} \right).\)

⦁ Ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) qua phép quay \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\)

Ta có \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\) biến điểm M khác O thành điểm M ₂ sao cho \(O{M_2}\; = {\rm{ }}OM{\rm{ }} = {\rm{ }}2\)và \((OM,{\rm{ }}O{M_2}){\rm{ }} = {\rm{ }}90^\circ \) nên \(\widehat {MO{M_2}} = 90^\circ \).

Suy ra tam giác \(MO{M_2}\) vuông cân tại O.

Ta có \(\widehat {{M_1}O{M_2}} = \widehat {MO{M_2}} - \widehat {MO{M_1}} = 90^\circ - 45^\circ = 45^\circ \)

Suy ra \(\widehat {MO{M_1}} = \widehat {{M_1}O{M_2}} = 45^\circ \)

Khi đó tam giác MOM ₂ có OM ₁ là đường phân giác.

Vì vậy OM ₁ cũng là đường trung trực của tam giác MOM ₂ hay Oy là đường trung trực của tam giác MOM ₂ .

Suy ra M ₂ là ảnh của điểm M qua phép đối xứng trục Oy.

Do đó hai điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) và M ₂ có cùng tung độ và có hoành độ đối nhau.

Vậy tọa độ \({M_2}\left( { - \sqrt 2 ;\sqrt 2 } \right)\)

⦁ Ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) qua phép quay \({Q_{(O,{\rm{ }}180^\circ )}}\)

Ta có \({Q_{(O,{\rm{ }}180^\circ )}}\) biến điểm M khác O thành điểm M ₃ sao cho \(O{M_3}\; = {\rm{ }}OM{\rm{ }} = {\rm{ }}2\)và \((OM,{\rm{ }}O{M_3}){\rm{ }} = {\rm{ }}180^\circ \) nên \(\widehat {MO{M_3}} = 180^\circ \)

Suy ra O là trung điểm của MM ₃ .

Khi đó \(\left\{ \begin{array}{l}{x_O} = \frac{{{x_M} + {x_{{M_3}}}}}{2}\\{y_O} = \frac{{{y_M} + {y_{{M_3}}}}}{2}\end{array} \right.\)

Vì vậy \(\left\{ \begin{array}{l}{x_{{M_3}}} = 2{x_O} - {x_M} = 2.0 - \sqrt 2 = - \sqrt 2 \\{y_{{M_3}}} = 2{y_O} - {y_M} = 2.0 - \sqrt 2 = - \sqrt 2 \end{array} \right.\)

Vậy tọa độ \({M_3}\left( { - \sqrt 2 ; - \sqrt 2 } \right)\)

⦁ Ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) qua phép quay \({Q_{(O,{\rm{ }}360^\circ )}}\)

Ta có \({Q_{(O,{\rm{ }}360^\circ )}}\) biến điểm M khác O thành điểm M ₄ sao cho \(O{M_4}\; = {\rm{ }}OM{\rm{ }} = {\rm{ }}2\)và \((OM,{\rm{ }}O{M_4}){\rm{ }} = {\rm{ }}360^\circ \) nên \(\widehat {MO{M_4}} = 360^\circ \)

Tức là, \({M_4}\; \equiv M.\)

Vậy tọa độ \({M_4}\left( {\sqrt 2 ;\sqrt 2 } \right)\).

Vận dụng 1

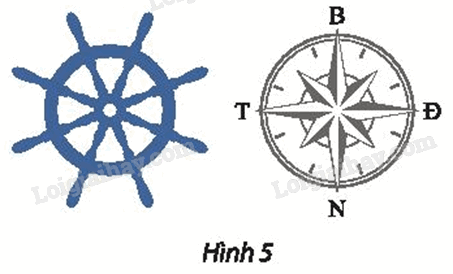
Một con tàu đang di chuyển theo hướng bắc. Người lái tàu phải thực hiện phép quay nào trên bánh lái để con tàu:

a) rẽ sang hướng tây?

b) rẽ sang hướng đông?