Giải mục 1 trang 71 SGK Toán 8 – Cánh diều
Cho
HĐ1
Cho tam giác ABC, điểm M nằm trên cạnh BC. Gọi A', B', C' lần lượt là trung điểm của các đoạn thẳng MA, MB, MC (Hình 47)
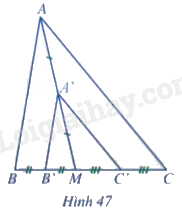
a) So sánh các cặp góc:
^B′A′C′ và ^BAC; ^C′B′A′ và ^CBA; ^A′C′B′ và ^ACB.
b) So sánh các tỉ số: A′B′AB; B′C′BC; C′A′CA.
Phương pháp giải:
a) Dựa vào tính chất đường trung bình của tam giác để so sánh các góc.
Sử dụng tính chất tổng các góc trong tam giác bằng 1800
b) Dựa vào tính chất đường trung bình để so sánh.
Lời giải chi tiết:
a) Xét tam giác ABM có A'B' là đường trung bình của tam giác
⇒A′B′//AB
⇒^C′B′A′=^CBA (hai góc đồng vị)
Tương tự, tam giác AMC có A'C' là đường trung bình nên ^A′C′B′=^ACB (hai góc đồng vị)
Xét tam giác ABC có:
^BAC+^CBA+^ACB=1800
Xét tam giác A'B'C' có:
^B′A′C′+^C′B′A′+^A′C′B′=1800
⇒^BAC+^CBA+^ACB=^B′A′C′+^C′B′A′+^A′C′B′
⇒^BAC=^B′A′C′
b) A'B' là đường trung bình của tam giác ABM nên
A′B′=12AB⇒A′B′AB=12
A'B' là đường trung bình của tam giác ABM nên
A′C′=12AC⇒A′C′AC=12
Ta có: B′C′BC=MB′+MC′2MB′+2MC′=MB′+MC′2(MB′+MC′)=12
⇒A′B′AB=B′C′BC=C′A′CA
LT1
Cho ΔA′B′C′∽ và AB = 3,\,\,BC = 2,\,\,CA = 4,\,\,A'B' = x,\,\,B'C' = 3,\,\,C'A' = y. Tìm x và y.
Phương pháp giải:
Sử dụng định nghĩa tam giác đồng dạng để tìm x và y.
Lời giải chi tiết:
Vì \Delta A'B'C' \backsim \Delta ABC nên ta có:
\left\{ \begin{array}{l}A'B' = AB = 3\\B'C' = BC = 2\end{array} \right.
Vậy x = 3 và y = 2.