Giải mục 2 trang 122, 123, 124 SGK Toán 11 tập 1 - Chân trời sáng tạo — Không quảng cáo

Hoạt động 2

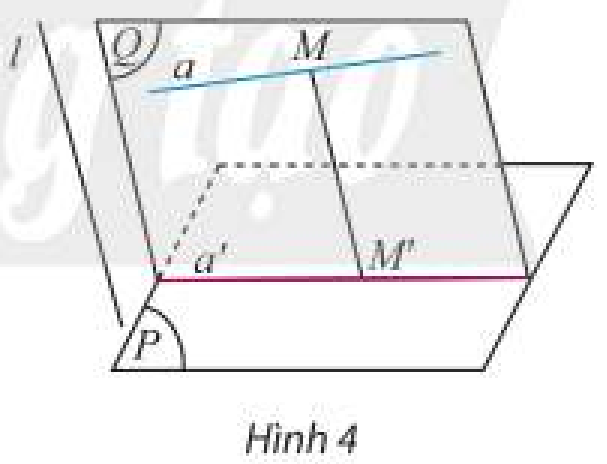
Trong Hình 4, xét phép chiếu theo phương $l$ lên mặt phẳng $\left( P \right)$, mặt phẳng $\left( Q \right)$ chứa đường thẳng $a$ và song song với phương chiếu.

a) Khi điểm $M$ thay đổi trên đường thẳng $a$ thì ảnh $M'$ của nó thay đổi ở đâu?

b) Từ đó hãy chỉ ra ảnh của đường thẳng $a$ qua phép chiếu theo phương $l$ lên mặt phẳng $\left( P \right)$.

Phương pháp giải:

Quan sát hình ảnh và trả lời câu hỏi.

Lời giải chi tiết:

a) Khi điểm $M$ thay đổi trên đường thẳng $a$ thì ảnh $M'$ của nó thay đổi trên đường thẳng $a'$.

b) Ảnh của đường thẳng $a$ qua phép chiếu theo phương $l$ lên mặt phẳng $\left( P \right)$ là đường thẳng $a'$.

Hoạt động 3

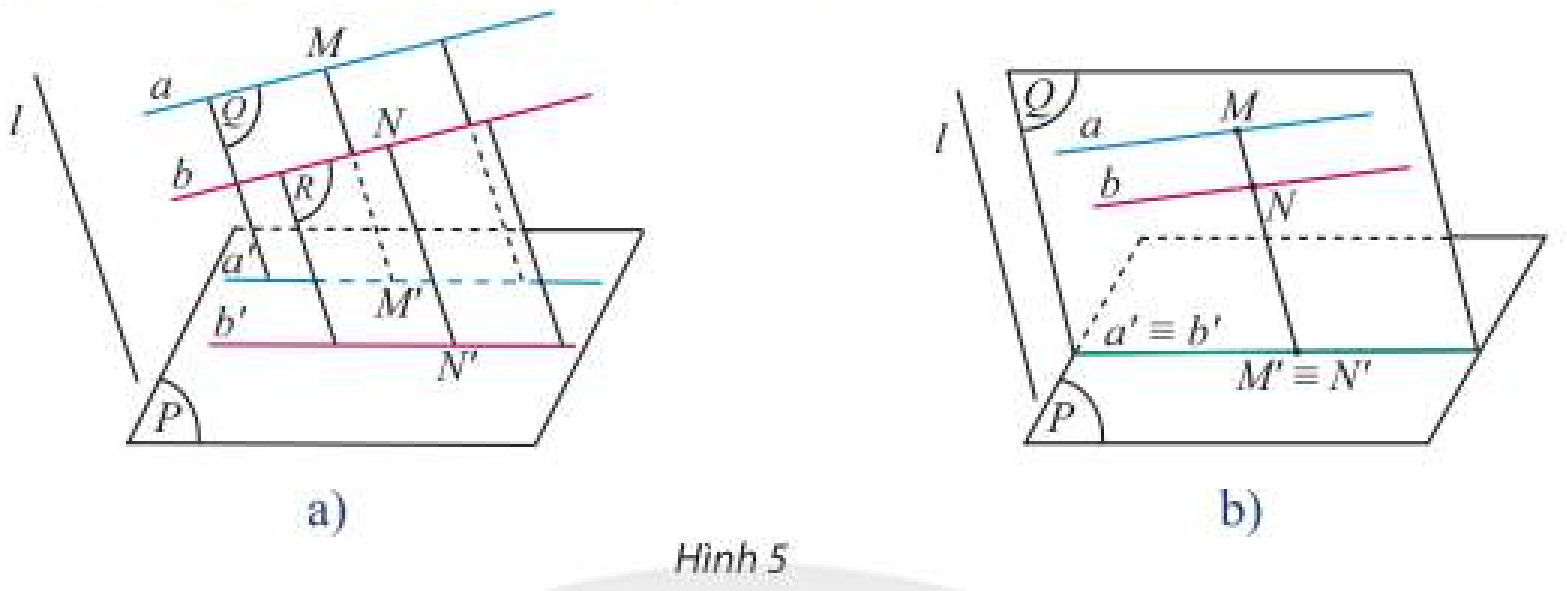
Trong Hình 5, xét phép chiếu theo phương $l$ với mặt phẳng chiếu $\left( P \right)$. Biết $a\parallel b$ với $a \subset \left( Q \right)$ và $b \subset \left( R \right)$. Nêu nhận xét về vị trí tương đối của hình chiếu $a',b'$ của $a,b$ trong hai trường hợp: $\left( Q \right)\parallel \left( R \right);\left( Q \right) \equiv \left( R \right)$.

Phương pháp giải:

‒ Quan sát hình ảnh và trả lời câu hỏi.

‒ Sử dụng định lí: Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ song song với nhau. Nếu $\left( R \right)$ cắt $\left( P \right)$ thì cắt $\left( Q \right)$ và hai giao tuyến của chúng song song.

Lời giải chi tiết:

Ta có:

$\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( P \right) \cap \left( Q \right) = a'\\\left( P \right) \cap \left( R \right) = b'\end{array} \right\} \Rightarrow a'\parallel b'$

Vậy nếu $\left( Q \right)\parallel \left( R \right)$ thì $a'\parallel b'$; nếu $\left( Q \right) \equiv \left( R \right)$ thì $a' \equiv b'$.

Thực hành 2

Cho hình thang $ABCD$ có đáy lớn $AB$ và $AB = 2CD$, hình chiếu song song của $ABCD$ là tứ giác $A'B'C'D'$. Chứng minh rằng $A'B'C'D'$ cũng là một hình thang và $A'B' = 2C'D'$.

Phương pháp giải:

Sử dụng tính chất của phép chiếu song song:

‒ Hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau.

‒ Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau.

Lời giải chi tiết:

$ABCD$ là hình thang có đáy lớn $AB \Rightarrow AB\parallel CD$.

Vì hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau, mà hình chiếu song song của $ABCD$ là tứ giác $A'B'C'D'$ nên $A'B'\parallel C'D'$. Vậy $A'B'C'D'$ cũng là một hình thang.

Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau, mà $AB = 2CD,AB\parallel CD$ và $A'B'\parallel C'D'$ nên $A'B' = 2C'D'$.

Vận dụng 2

Cho $G$ là trọng tâm tam giác $ABC$, $M$ là trung điểm $BC$ và hình chiếu song song của tam giác $ABC$ là tam giác $A'B'C'$. Chứng minh rằng hình chiếu $M'$ của $M$ là trung điểm của $B'C'$ và hình chiếu $G'$ của $G$ cũng là trọng tâm tam giác $A'B'C'$.

Phương pháp giải:

Sử dụng tính chất của phép chiếu song song:

‒ Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.

‒ Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau.

Lời giải chi tiết:

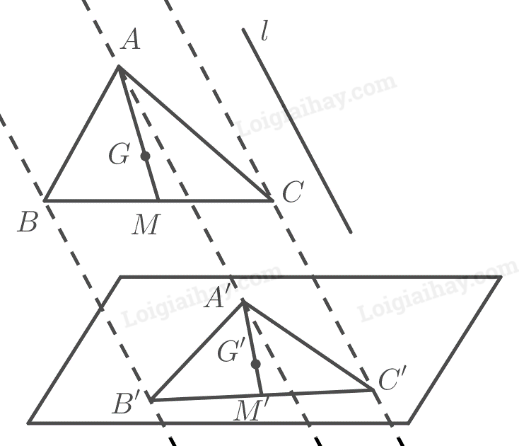
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có $M$ nằm giữa $B$ và $C$ thì $M'$ nằm giữa $B'$ và $C'$.

Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có $MB = MC$ thì $M'B' = M'C'$.

Vậy $M'$ là trung điểm của $B'C'$.

Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có $G$ nằm giữa $A$ và $M$ thì $G'$ nằm giữa $A'$ và $M'$.

Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có $AG = \frac{2}{3}AM$ thì $A'G' = \frac{2}{3}A'M'$.

Vậy $G'$ là trọng tâm tam giác $A'B'C'$.