Giải mục 2 trang 102, 103, 104, 105 SGK Toán 11 tập 1 - Chân trời sáng tạo — Không quảng cáo

Hoạt động 2

a) Trong không gian, cho điểm $M$ ở ngoài đường thẳng $d$. Đặt $\left( P \right) = mp\left( {M,d} \right)$. Trong $\left( P \right)$, qua $M$ vẽ đường thẳng $d'$ song song với $d$, đặt $\left( Q \right) = mp\left( {d,d'} \right)$. Có thể khẳng định hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ trùng nhau không?

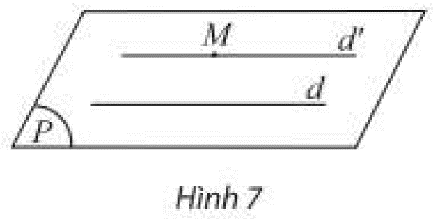
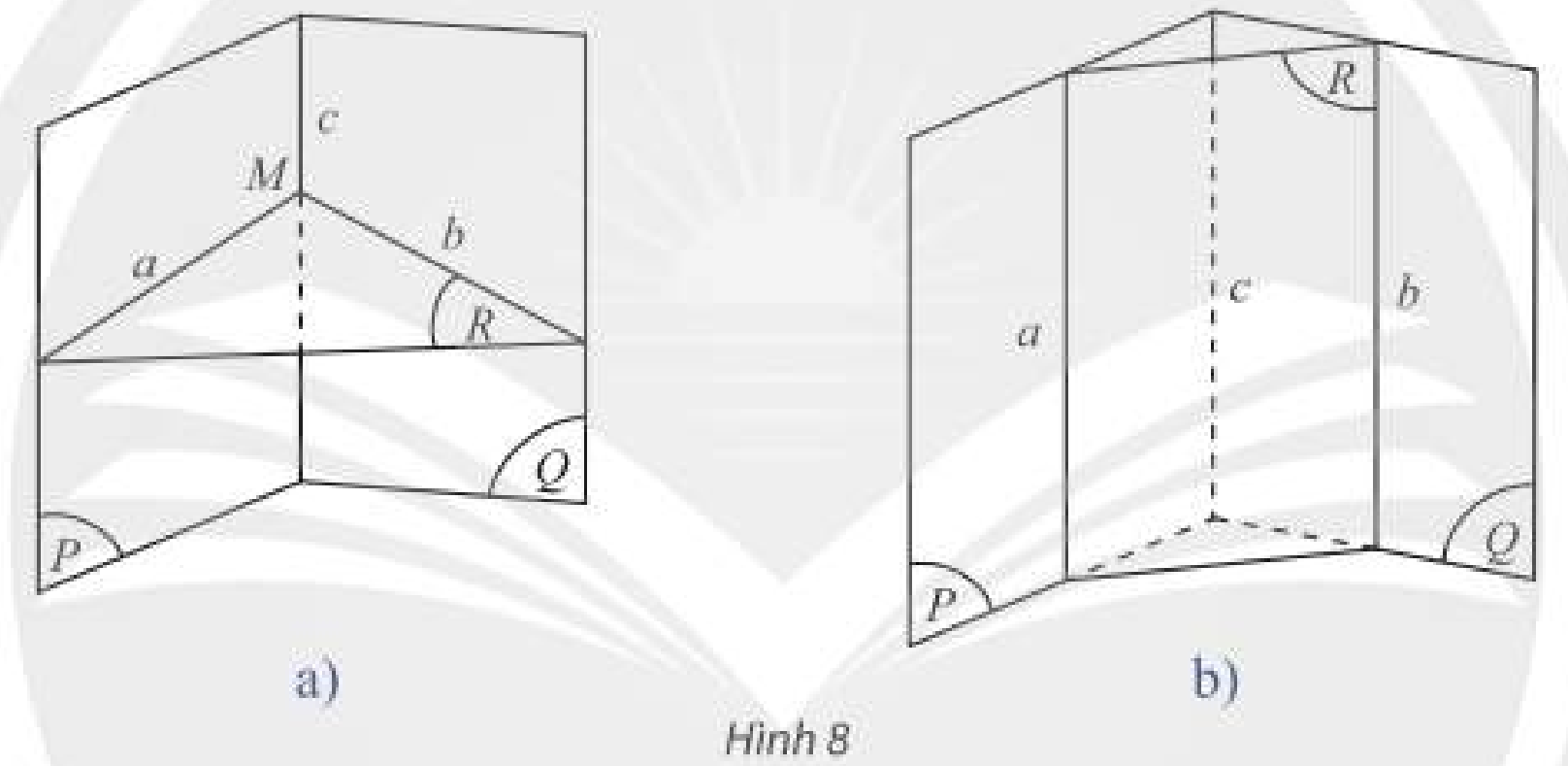
b) Cho ba mặt phẳng $\left( P \right),\left( Q \right),\left( R \right)$ cắt nhau theo ba giao tuyến $a,b,c$ phân biệt với $a = \left( P \right) \cap \left( R \right);b = \left( Q \right) \cap \left( R \right);c = \left( P \right) \cap \left( Q \right)$ (Hình 8).

Nếu $a$ và $b$ có điểm chung $M$ thì điểm $M$ có thuộc $c$ không?

Phương pháp giải:

Áp dụng tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.

Lời giải chi tiết:

a) Theo đề bài ta có: $d' \subset \left( P \right),d' \subset \left( Q \right)$ nên $d'$ là giao tuyến của hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$.

Lại có: $d \subset \left( P \right),d \subset \left( Q \right)$ nên $d$ cũng là giao tuyến của hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$.

Theo tính chất thừa nhận 5: hai mặt phẳng phân biệt có một đường thẳng chung duy nhất. Vậy hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ trùng nhau.

b) Ta có:

$\begin{array}{l}\left. \begin{array}{l}M \in a\\a \subset \left( P \right)\end{array} \right\} \Rightarrow M \in \left( P \right)\\\left. \begin{array}{l}M \in b\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow M \in \left( Q \right)\end{array}$

Do đó điểm $M$ nằm trên giao tuyến của hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$. Vậy $M \in c$.

Thực hành 2

Cho hình chóp $S.ABCD$. Vẽ hình thang $A{\rm{D}}M{\rm{S}}$ có hai đáy là $A{\rm{D}}$ và $M{\rm{S}}$. Gọi $d$ là đường thẳng trong không gian đi qua ${\rm{S}}$ và song song với $A{\rm{D}}$. Chứng minh đường thẳng $d$ nằm trong mặt phẳng $\left( {SAD} \right)$.

Phương pháp giải:

Sử dụng:

‒ Định lí 1: Trong không gian, qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó.

‒ Tính chất: Có duy nhất một mặt phẳng chứa hai đường thẳng song song.

Lời giải chi tiết:

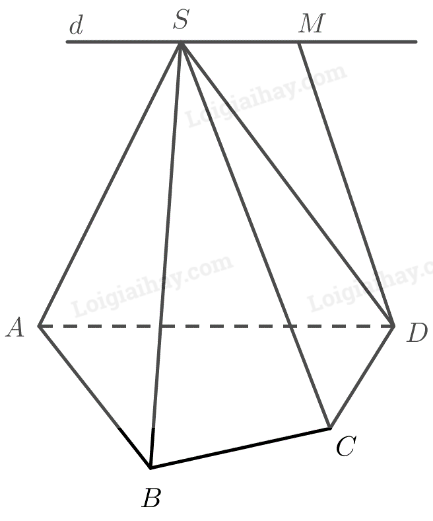
$A{\rm{D}}M{\rm{S}}$ là hình thang có hai đáy là $A{\rm{D}}$ và $M{\rm{S}}$ nên $A{\rm{D}}\parallel M{\rm{S}}$.

Theo đề bài ta lại có $d\parallel A{\rm{D}}$.

Do đó $d \equiv MS$ (theo định lí 1).

Lại có: $SM \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {SA{\rm{D}}} \right)$.

Hoạt động 3

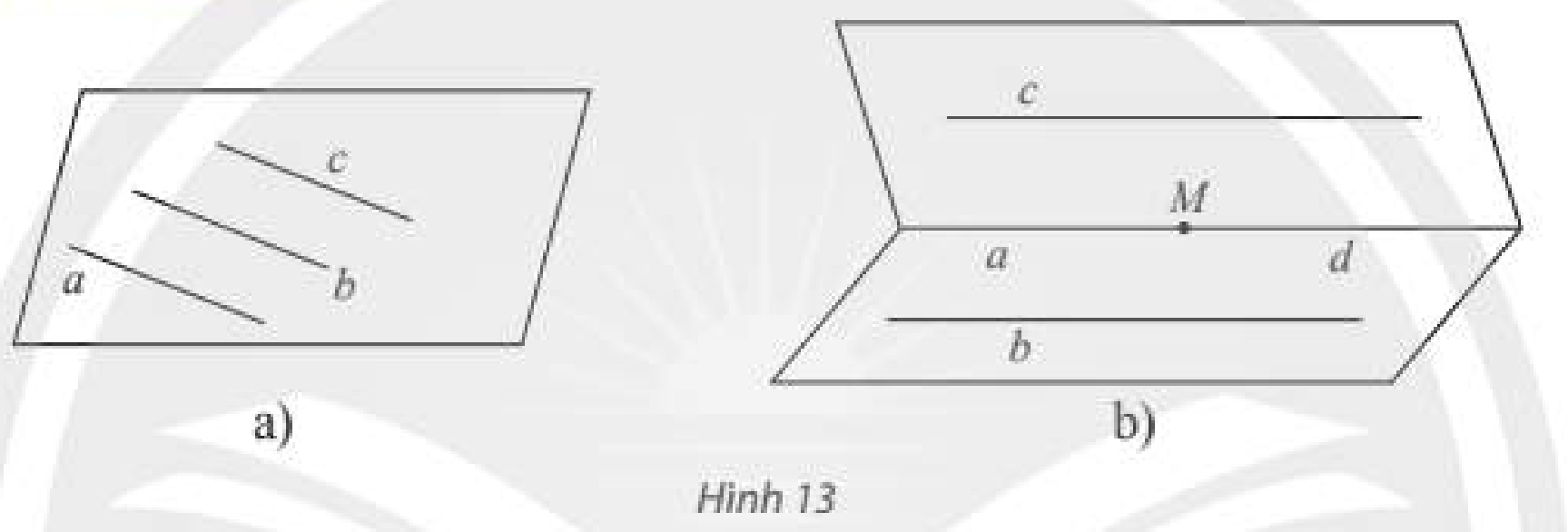
Ta đã biết trong cùng một mặt phẳng, hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau (Hình 13a).

Trong không gian, cho ba đường thẳng  không đồng phẳng, $a$ và $b$ cùng song song với $c$. Gọi $M$ là điểm thuộc $a$, $d$ là giao tuyến của $mp\left( {a,c} \right)$ và $mp\left( {M,b} \right)$ (Hình 13b). Do $b\parallel c$ nên ta có $d\parallel b$ và $d\parallel c$. Giải thích tại sao $d$ phải trùng với $a$. Từ đó, nêu kết luận về vị trí giữa $a$ và $b$.

Phương pháp giải:

Sử dụng định lí 1: Trong không gian, qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó.

Lời giải chi tiết:

Ta có: $d = mp\left( {a,c} \right) \cap mp\left( {M,b} \right) \Rightarrow M \in d$

Lại có: $M \in a$

Mà qua $M$ chỉ có một đường thẳng song song với đường thẳng $b$ nên $d \equiv a$.

Do đó $a\parallel b$.

Thực hành 3

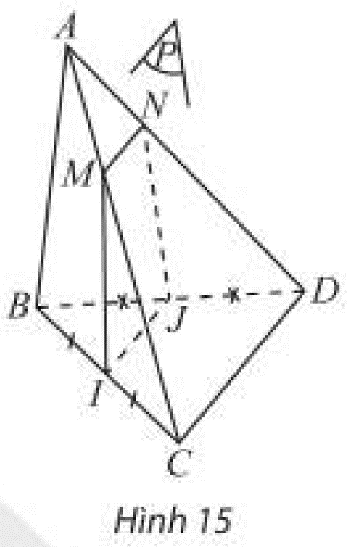
Cho tứ diện $ABCD$ có $I$ và $J$ lần lượt là trung điểm của các cạnh $BC$ và $B{\rm{D}}$. Gọi $\left( P \right)$ là mặt phẳng đi qua $I,J$ và cắt hai cạnh $AC$ và $A{\rm{D}}$ lần lượt tại $M$ và $N$.

a) Chứng minh $IJNM$ là một hình thang.

b) Tìm vị trí của điểm $M$ dễ $IJNM$ là hình bình hành.

Phương pháp giải:

Sử dụng định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đổi một song song.

Lời giải chi tiết:

a) Ta có: $I$ là trung điểm của $BC$

$J$ là trung điểm của $B{\rm{D}}$

$\Rightarrow IJ$ là đường trung bình của tam giác $BCD$

$\Rightarrow IJ\parallel CD,IJ = \frac{1}{2}C{\rm{D}}$

Ta có:

$\begin{array}{l}IJ = \left( {BC{\rm{D}}} \right) \cap \left( P \right)\\MN = \left( {AC{\rm{D}}} \right) \cap \left( P \right)\\C{\rm{D}} = \left( {AC{\rm{D}}} \right) \cap \left( {BC{\rm{D}}} \right)\\IJ\parallel C{\rm{D}}\end{array}$

Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: $IJ\parallel MN\parallel C{\rm{D}}$.

Vậy $IJNM$ là hình thang.

b) Để $IJNM$ là hình bình hành thì $IJ = MN$.

Mà $IJ = \frac{1}{2}CD$ nên $MN = \frac{1}{2}CD$.

Khi đó $MN$ là đường trung bình của tam giác $ACD$.

$\Rightarrow M$ trung điểm của AC.

Vận dụng 2

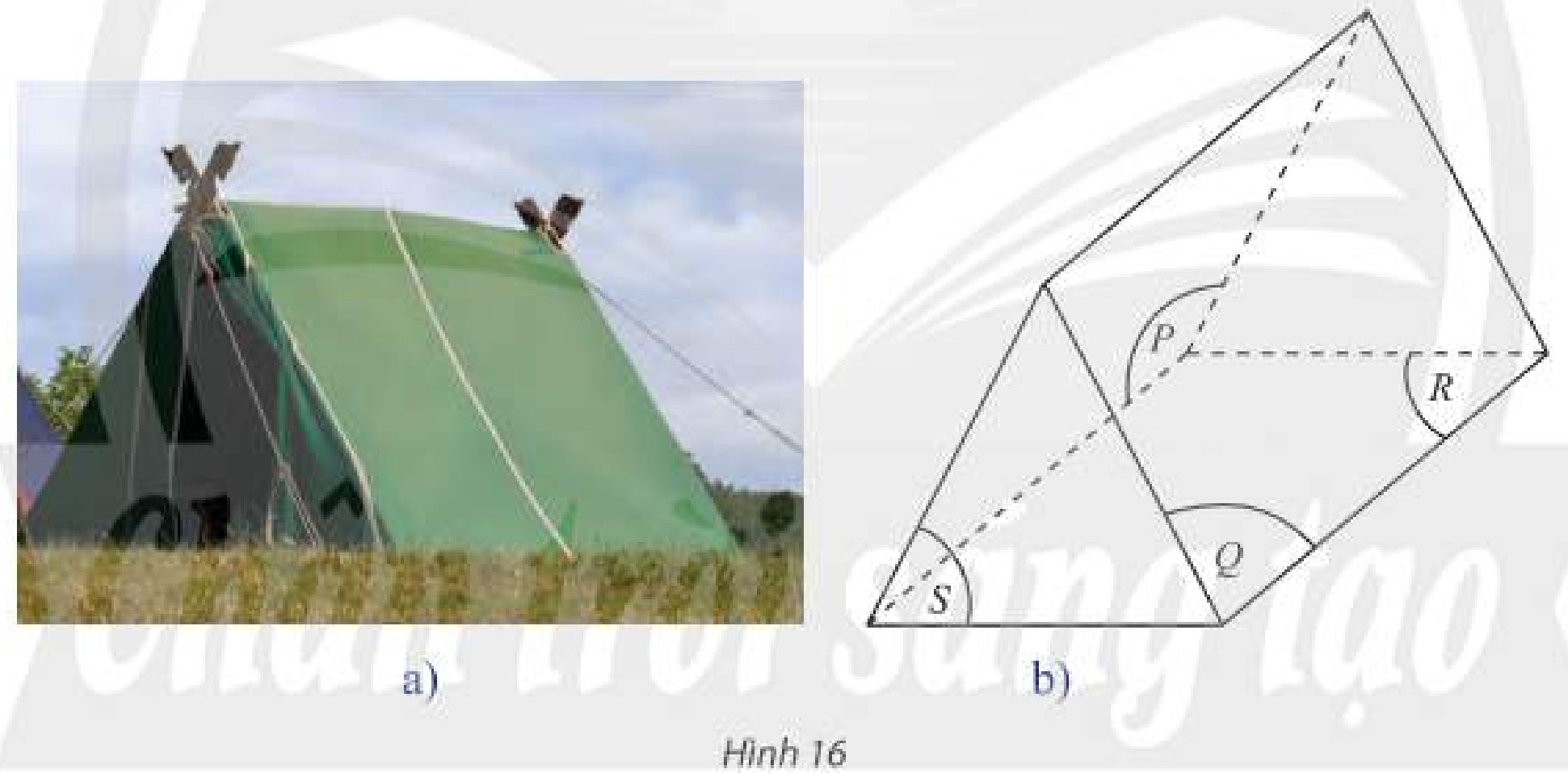
Một chiếc lều (Hình 16a) được minh hoạ như Hình 16b.

a) Tìm ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến song song.

b) Tìm ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến đồng quy.

Phương pháp giải:

Áp dụng định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.

Lời giải chi tiết:

a) Ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến song song là: $\left( P \right),\left( Q \right),\left( R \right)$.

b) Ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến đồng quy là: $\left( P \right),\left( Q \right),\left( S \right)$.