Giải mục 2 trang 32, 33, 34, 35 SGK Toán 8 tập 2 – Chân trời sáng tạo
Xét cân thăng bằng ở khởi động a) Giải thích tại sao nếu bỏ ra khỏi mỗi đĩa cân một quả cân (x) gam thì cân vẫn thăng bằng. b) Nếu thay quả cân 600 gam bằng quả cân 200 gam (Hình 2) thì cân còn thăng bằng không? Tại sao? c) Tiếp theo, chia các quả cân trên mỗi cân thành ba phần bằng nhau, rồi bỏ ra hai phần (hình 3). Khi đó, cân còn thằng bằng không? Tại sao?
HĐ2
Xét cân thăng bằng ở khởi động
a) Giải thích tại sao nếu bỏ ra khỏi mỗi đĩa cân một quả cân \(x\) gam thì cân vẫn thăng bằng.
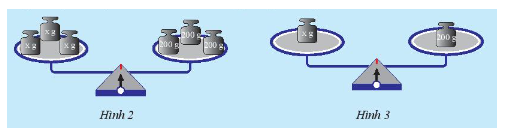
b) Nếu thay quả cân 600 gam bằng quả cân 200 gam (Hình 2) thì cân còn thăng bằng không? Tại sao?
c) Tiếp theo, chia các quả cân trên mỗi cân thành ba phần bằng nhau, rồi bỏ ra hai phần (hình 3). Khi đó, cân còn thằng bằng không? Tại sao?
Phương pháp giải:
- Dựa vào quy tắc khi ta cộng hoặc trừ cả hai vế cho một số.
Lời giải chi tiết:
a) Sở dĩ khi bỏ ra khỏi mỗi đĩa cân một quả cân là \(x\) thì cân vẫn thằng bằng vì cả hai bên đĩa cân đều trừ đi một lượng giống nhau là \(x\)gam.
b) Nếu thay quả cân 600 gam bằng qủa cân 200 gam thì cân vẫn cân bằng vì tổng khối lượng 3 quả cân 200 gam là 600 gam.
c) Cân vẫn cân bằng, vì chia đều.
TH2
Giải các phương trình sau:
a) \(\dfrac{2}{3}x + 1\dfrac{1}{2} = 0\);
b) \(2\dfrac{1}{2} - 0,75x = 0\).
Phương pháp giải:
Sử dụng các quy tắc:
- Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế);
- Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
- Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
Lời giải chi tiết:
a) \(\dfrac{2}{3}x + 1\dfrac{1}{2} = 0\)
\(\dfrac{2}{3}x + \dfrac{3}{2} = 0\)
\(\dfrac{2}{3}x = 0 - \dfrac{3}{2}\) (quy tắc chuyển vế)
\(\dfrac{2}{3}x = \dfrac{{ - 3}}{2}\)
\(x = \dfrac{{ - 3}}{2}:\dfrac{2}{3}\) (quy tắc chia cho một số)
\(x = \dfrac{{ - 9}}{4}\)
Vậy phương trình có nghiệm \(x = \dfrac{{ - 9}}{4}\).
b) \(2\dfrac{1}{2} - 0,75x = 0\)
\(\dfrac{5}{2} - 0,75x = 0\)
\( - 0,75x = 0 - \dfrac{5}{2}\) (quy tắc chuyển vế)
\( - 0,75x = - \dfrac{5}{2}\)
\(x = \left( { - \dfrac{5}{2}} \right):\left( { - 0,75} \right)\) (quy tắc chia cho một số)
\(x = \dfrac{{10}}{3}\)
Vậy phương trình có nghiệm \(x = \dfrac{{10}}{3}\).
TH3
Giải các phương trình sau:
a) \(15 - 4x = x - 5\);
b) \(\dfrac{{5x + 2}}{4} + \dfrac{{3x - 2}}{3} = \dfrac{3}{2}\).
Phương pháp giải:
- Quy đồng mẫu số.
- Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế);
- Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
- Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
Lời giải chi tiết:
a) \(15 - 4x = x - 5\)
\( - 4x - x = - 5 - 15\) (chuyển vế)
\( - 5x = - 20\)
\(x = \left( { - 20} \right):\left( { - 5} \right)\) (chia cho một số)
\(x = 4\)
Vậy phương trình có nghiệm \(x = 4\).
b) \(\dfrac{{5x + 2}}{4} + \dfrac{{3x - 2}}{3} = \dfrac{3}{2}\)
\(\dfrac{{\left( {5x + 2} \right).3}}{{4.3}} + \dfrac{{\left( {3x - 2} \right).4}}{{3.4}} = \dfrac{{3.6}}{{2.6}}\) (quy đồng mẫu số)
\(\dfrac{{15x + 6}}{{12}} + \dfrac{{12x - 8}}{{12}} = \dfrac{{18}}{{12}}\)
\(15x + 6 + 12x - 8 = 18\) (chia cả hai vế cho một số)
\(15x + 12x = 18 - 6 + 8\) (chuyển vế)
\(27x = 20\) (rút gọn)
\(x = 20:27\) (chia cả hai vế co một số)
\(x = \dfrac{{20}}{{27}}\)
Vậy phương trình có nghiệm \(x = \dfrac{{20}}{{27}}\).
VD2
Hai bạn An và Mai giải phương trình \(x = 2x\) như sau:
An: \(x = 2x\)
\(1 = 2\) (chia cả hai vế cho \(x\))
Vậy phương trình vô nghiệm.
Mai: \(x = 2x\)
\(x - 2x = 0\) (chuyển \(2x\) sang vế trái)
\( - x = 0\) (rút gọn)
\(x = 0\) (nhân hai vế với –1)
Vậy phương trình đã cho có nghiệm \(x = 0\).
Em hãy cho biết bạn nào giải đúng.
Phương pháp giải:
Khi chia cả hai vế cho một số thì số đó phải khác 0.
Lời giải chi tiết:
Bạn Mai giải đúng và bạn An giải sai vì khi bạn An chia cả hai vế cho \(x\) thì chưa đảm bảo tính số chia khác 0 do chúng ta chưa biết \(x\).