Giải mục 2 trang 35, 36, 37 Chuyên đề học tập Toán 10 - Chân trời sáng tạo — Không quảng cáo

HĐ Khám phá 2

Từ các đẳng thức như

\(\begin{array}{l}C_3^0 = C_3^3 = 1,\quad C_4^1 = C_4^3 = 4,\\C_3^0 + C_3^1 = C_4^1,\quad C_4^2 + C_4^3 = C_5^3,\end{array}\)

Có thể dự đoán rằng, với mỗi \(n \in \mathbb{N}*\),

\(\begin{array}{l}C_n^k = C_n^{n - k}\quad \quad \quad (0 \le k \le n)\quad (2)\\C_n^{k - 1} + C_n^k = C_{n + 1}^k\quad (1 \le k \le n)\quad (3)\end{array}\)

Hãy chứng minh các công thức trên.

Gợi ý: Sử dụng công thức \(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}},n \in \mathbb{N},0 \le k \le n.\)

Lời giải chi tiết:

\(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}} = \frac{{n!}}{{\left( {n - k} \right)!k!}} = \frac{{n!}}{{\left( {n - k} \right)!\left[ {n - (n - k)} \right]!}} = C_n^{n - k}\)

\(\begin{array}{l}C_n^{k - 1} + C_n^k = \frac{{n!}}{{(k - 1)!\left( {n - k + 1} \right)!}} + \frac{{n!}}{{k!\left( {n - k} \right)!}}\\ = \frac{{n!}}{{k!\left( {n + 1 - k} \right)!}}\left( {k + \left( {n + 1 - k} \right)} \right)\\ = \frac{{(n + 1)!}}{{k!\left( {n + 1 - k} \right)!}} = C_{n + 1}^k\end{array}\)

Thực hành 2

Sử dụng tam giác Pascal, hãy khai triển:

a) \({(2x + 1)^6}\)

b) \({(x - y)^7}\)

Phương pháp giải:

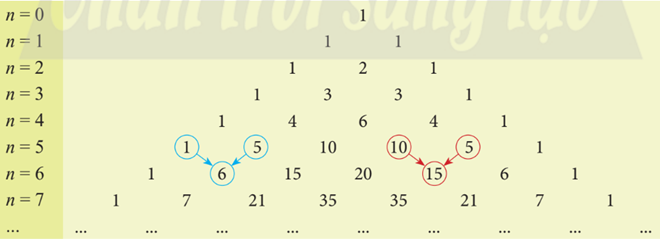
Lời giải chi tiết:

a) Sử dụng tam giác Pascal, ta có:

\(\begin{array}{l}{(2x + 1)^6} = {\left( {2x} \right)^6} + 6{\left( {2x} \right)^5} + 15{\left( {2x} \right)^4} + 20{\left( {2x} \right)^3} + 15{\left( {2x} \right)^2} + 6.2x + 1\\ = 64{x^6} + 192{x^5} + 240{x^4} + 160{x^3} + 60{x^2} + 12x + 1\end{array}\)

b) Sử dụng tam giác Pascal, ta có:

\(\begin{array}{l}{(x + ( - y))^7} = {x^7} + 7{x^6}( - y) + 21{x^5}{( - y)^2} + 35{x^4}{( - y)^3} + 35{x^3}{( - y)^4} + 21{x^2}{( - y)^5} + 7x{( - y)^6} + {( - y)^7}\\ = {x^7} - 7{x^6}y + 21{x^5}{y^2} - 35{x^4}{y^3} + 35{x^3}{y^4} - 21{x^2}{y^5} + 7x{y^6} - {y^7}\end{array}\)