Giải mục 2 trang 52, 53 Chuyên đề học tập Toán 10 - Chân trời sáng tạo — Không quảng cáo

HĐ2

Cho điểm $M(x;y)$nằm trên hypebol (H): $\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1$

a) Chứng minh rằng ${F_1}{M^2} - {F_2}{M^2} = 4cx$

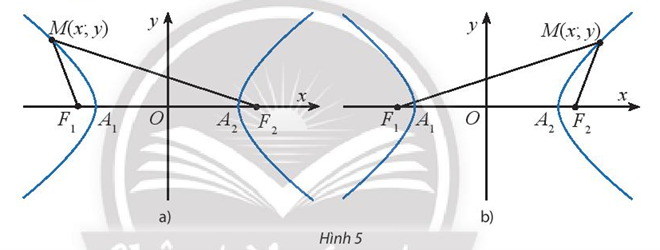
b) Giả sử điểm $M(x;y)$ thuộc nhánh đi qua ${A_1}( - a;0)$ (Hình 5a). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất $M{F_2} - M{F_1} = 2a$ đã biết để chứng minh $M{F_2} + M{F_1} =  - 2\frac{{cx}}{a}$. Từ đó, chứng minh các công thức: $M{F_1} =  - a - \frac{c}{a}{x_0};M{F_2} = a - \frac{c}{a}{x_0}$

b) Giả sử điểm $M(x;y)$ thuộc nhánh đi qua ${A_2}(a;0)$ (Hình 5b). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất $M{F_1} - M{F_2} = 2a$ đã biết để chứng minh $M{F_2} + M{F_1} = 2\frac{{cx}}{a}$. Từ đó, chứng minh các công thức: $M{F_1} = a + \frac{c}{a}{x_0};M{F_2} =  - a + \frac{c}{a}{x_0}$

Lời giải chi tiết:

a) Tính $M{F_1}^2 - M{F_2}^2$

Ta có: $\overrightarrow {F{M_1}} (x + c;y);\overrightarrow {{F_2}M} (x - c;y)$

$\Rightarrow {F_1}{M^2} = {(x + c)^2} + {y^2};M{F_2}^2 = {(x - c)^2} + {y^2}$

$\Rightarrow {F_1}{M^2} - {F_2}{M^2} = {(x + c)^2} - {(x - c)^2} = 4c{x_0}$

b) Khi điểm $M({x_0};{y_0})$ thuộc nhánh chứa đỉnh ${A_1}( - a;0)$ ($M{F_2} - M{F_1} = 2a$),

$\begin{array}{l}M{F_1} + M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} - M{F_2}}} =  - \frac{{2c}}{a}x\\M{F_1} = \frac{{\left( { - \frac{{2c}}{a}x} \right) - 2a}}{2} =  - a - \frac{c}{a}x\\M{F_2} = \frac{{\left( { - \frac{{2c}}{a}x} \right) + 2a}}{2} = a - \frac{c}{a}x\end{array}$

c) Khi điểm $M(x;y)$ thuộc nhánh chứa đỉnh ${A_2}(a;0)$ ($M{F_1} - M{F_2} = 2a$),

$\begin{array}{l}M{F_1} + M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} - M{F_2}}} = \frac{{2c}}{a}x\\M{F_1} = \frac{{\frac{{2c}}{a}x + 2a}}{2} = a + \frac{c}{a}x\\M{F_2} = \frac{{\frac{{2c}}{a}x - 2a}}{2} =  - a + \frac{c}{a}x\end{array}$

Thực hành 2

Tính độ dài hai bán kính qua tiêu của điểm $M(x;y)$ trên hypebol (H): $\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1$

Phương pháp giải:

Cho điểm $M(x;y)$nằm trên hypebol (H): $\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1$

Độ dài hai bán kính qua tiêu của điểm $M(x;y)$ là:

$M{F_1} = \left| {a + \frac{c}{a}x} \right|;M{F_2} = \left| {a - \frac{c}{a}x} \right|$

Lời giải chi tiết:

Hypebol (H): $\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1$ có $a = 8,b = 6$ suy ra $c = \sqrt {{a^2} + {b^2}}  = 10$.

Độ dài hai bán kính qua tiêu của điểm $M(x;y)$ là:

$M{F_1} = \left| {a + \frac{c}{a}x} \right| = \left| {8 + \frac{3}{4}x} \right|;M{F_2} = \left| {a - \frac{c}{a}x} \right| = \left| {8 - \frac{3}{4}x} \right|$

Vận dụng 2

Tính độ dài hai bán kính qua tiêu của đỉnh ${A_2}(a;0)$ trên hypebol (H): $\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1$

Phương pháp giải:

Cho điểm $M(x;y)$nằm trên hypebol (H): $\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1$

Độ dài hai bán kính qua tiêu của điểm $M(x;y)$ là:

$M{F_1} = \left| {a + \frac{c}{a}x} \right|;M{F_2} = \left| {a - \frac{c}{a}x} \right|$

Lời giải chi tiết:

Độ dài hai bán kính qua tiêu của điểm ${A_2}(a;0)$ trên (H) là:

$M{F_1} = \left| {a + \frac{c}{a}x} \right| = \left| {a + \frac{c}{a}a} \right| = a + c;M{F_2} = \left| {a - \frac{c}{a}x} \right| = \left| {a - \frac{c}{a}a} \right| = c - a.$