Giải mục 2 trang 51 SGK Toán 12 tập 2 - Kết nối tri thức — Không quảng cáo

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 51 SGK Toán 12 Kết nối tri thức

Trong không gian Oxyz, cho đường thẳng \(\Delta \) và mặt phẳng (P). Xét \(\overrightarrow u  = \left( {a;b;c} \right)\) là một vectơ chỉ phương của \(\Delta \) và \(\overrightarrow n  = \left( {A;B;C} \right)\) (với giá \(\Delta '\)) là một vectơ pháp tuyến của (P). (H.5.35)

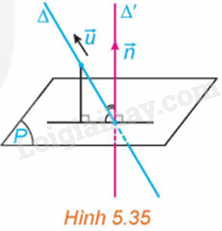
a) Hãy tìm mối quan hệ giữa các góc \(\left( {\Delta ,\left( P \right)} \right)\) và \(\left( {\Delta ,\Delta '} \right)\).

b) Có nhận xét gì về mối quan hệ giữa \(\sin \left( {\Delta ,\Delta '} \right)\) và \(\left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|\)?

Phương pháp giải:

Sử dụng kiến thức giá của vectơ để chứng minh: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ đó.

Lời giải chi tiết:

a) Mối quan hệ của góc \(\left( {\Delta ,\left( P \right)} \right)\) và \(\left( {\Delta ,\Delta '} \right)\) là: \(\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta '} \right)\)

b) Ta có: +) \(\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta '} \right) = {90^0} - \left( {\overrightarrow u ,\overrightarrow n } \right)\) với \(\left( {\overrightarrow u ,\overrightarrow n } \right) \le {90^o}\)

+) \(\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta '} \right) = {90^0} - \left[ {{{180}^o} - \left( {\overrightarrow u ,\overrightarrow n } \right)} \right] =  - {90^o} + \left( {\overrightarrow u ,\overrightarrow n } \right)\) với \(\left( {\overrightarrow u ,\overrightarrow n } \right) > {90^o}\)

Suy ra, \(\sin \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|\).

LT2

Trả lời câu hỏi Luyện tập 2 trang 51 SGK Toán 12 Kết nối tri thức

Trong không gian Oxyz, tính góc giữa đường thẳng \(\Delta \) và mặt phẳng (P), với:

\(\Delta :\frac{{x + 2}}{{ - 1}} = \frac{{y - 4}}{2} = \frac{{z + 1}}{1},\left( P \right):x - y + z - 1 = 0\).

Phương pháp giải:

Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính: Trong không gian Oxyz, cho đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u  = \left( {a;b;c} \right)\) và mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n  = \left( {A;B;C} \right)\).

Khi đó: \(\sin \left( {\Delta ,\left( P \right)} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right| = \frac{{\left| {aA + bB + cC} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {{A^2} + {B^2} + {C^2}} }}\)

Lời giải chi tiết:

Đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u  = \left( { - 1;2;1} \right)\), mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n  = \left( {1; - 1;1} \right)\). Ta có: \(\sin \left( {\Delta ,\left( P \right)} \right) = \frac{{\left| {\left( { - 1} \right).1 + 2.\left( { - 1} \right) + 1.1} \right|}}{{\sqrt {{{\left( { - 1} \right)}^2} + {2^2} + {1^2}} .\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \frac{{\sqrt 2 }}{3}\)

Do đó, góc giữa đường thẳng \(\Delta \) và mặt phẳng (P) khoảng \(28,{1^0}\).