Giải mục 2 trang 68,69,70 SGK Toán 12 tập 1 - Cánh diều — Không quảng cáo

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 68 SGK Toán 12 Cánh diều

Cho điểm M trong không gian với hệ tọa độ Oxyz

a) Vẽ vecto $\overrightarrow {OM}$

b) Nêu cách xác định tọa độ của điểm M

Lời giải chi tiết:

a)

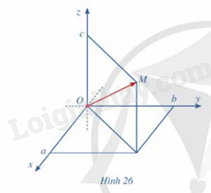
b) Nếu $\;\overrightarrow {OM}$ có tọa độ (a;b;c) thì ta viết $\;\overrightarrow {OM}$ = (a;b;c), trong đó a là hoành độ, b là tung độ và c là cao độ

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 69 SGK Toán 12 Cánh diều

Trong không gian với hệ tọa độ Oxyz, cho vecto $\vec u\;$(hình 28). Hãy xác định điểm A sao cho $\overrightarrow {OA}  = \vec u$

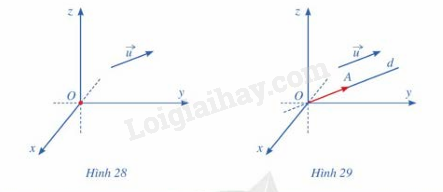
Phương pháp giải:

Vẽ $\overrightarrow {OA\;}$có tung độ, hoành độ và cao độ giống nhau

Lời giải chi tiết:

$\overrightarrow {OA}  = \vec u$ khi cả hai có chung tung độ hoành độ và cao độ bằng nhau

HĐ5

Trả lời câu hỏi Hoạt động 5 trang 70 SGK Toán 12 Cánh diều

Trong không gian với hệ tọa độ Oxyz, cho vecto $\vec u = \left( {a;b;c} \right)$( hình 31)

Lấy điểm A sao cho $\overrightarrow {OA}  = \vec u$.

a)     Tìm hoành độ, tung độ và cao độ của điểm A

b)    Biểu diễn vecto $\overrightarrow {OH}$ qua vecto$\;\vec i$  vecto $\overrightarrow {OK}$ qua vecto $\vec j$ ,vecto $\overrightarrow {OP}$qua vecto $\vec k$

c)     Biểu diễn vecto $\vec u\;$theo các vecto $\vec i,\vec j,\vec k$

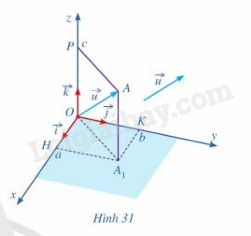
Phương pháp giải:

Áp dụng quy tắc các tọa độ của vecto

Lời giải chi tiết:

a)Ox là hoành độ của điểm A

Oy là  tung dộ của điểm A

Oz là cao độ của điểm A

$b)\overrightarrow {OH}  = \overrightarrow {ai}$

$\overrightarrow {OK}  = \overrightarrow {jb}$

$\overrightarrow {OP}  = \overrightarrow {kc}$

c) $\vec u = \overrightarrow {OA}  = \overrightarrow {OH}  + \overrightarrow {OK}$

=> $\vec u = \overrightarrow {ai}  + \overrightarrow {bj}$

HĐ6

Trả lời câu hỏi Hoạt động 6 trang 71 SGK Toán 12 Cánh diều

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})$

a.Biểu diễn mỗi vecto $\overrightarrow {OA} ,\overrightarrow {OB}$ theo các vecto $\overrightarrow i ,\overrightarrow j$ và $\overrightarrow k$

b. Tìm liên hệ giữa $\overrightarrow {AB}$ và  $({x_B} - {x_A}).\vec i + ({y_B} - {y_A}).\vec j + ({z_B} - {z_A}).\vec k$

c. Từ đó, tìm tọa độ vecto $\overrightarrow {AB}$

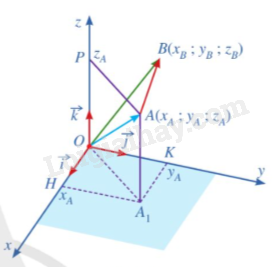
Phương pháp giải:

Sử dụng lý thuyết tọa độ của vecto trong không gian

Lời giải chi tiết:

a) $\overrightarrow {OA}  = \overrightarrow {O{A_1}}  + \overrightarrow {OP}  = \overrightarrow {OH}  + \overrightarrow {OK}  = {x_A}.\overrightarrow i  + {y_A}.\overrightarrow j  + {z_A}.\overrightarrow k$

Tương tự, ta có: $\overrightarrow {OB}  = {x_B}.\overrightarrow i  + {y_B}.\overrightarrow j  + {z_B}.\overrightarrow k$

b) Ta có: $\overrightarrow {AB}  = \overrightarrow {OB}  - \overrightarrow {OA}  = {x_B}.\overrightarrow i  + {y_B}.\overrightarrow j  + {z_B}.\overrightarrow k  - ({x_A}.\overrightarrow i  + {y_A}.\overrightarrow j  + {z_A}.\overrightarrow k ) = ({x_B} - {x_A}).\overrightarrow i  + ({y_B} - {y_A}).\overrightarrow j  + ({z_B} - {z_A}).\overrightarrow k$

c)Tọa độ vecto $\overrightarrow {AB} ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})$