Giải mục 2 trang 22, 23, 24 SGK Toán 12 tập 1 - Cánh diều
Đường tiệm cận đứng
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 22 SGK Toán 12 Cánh diều
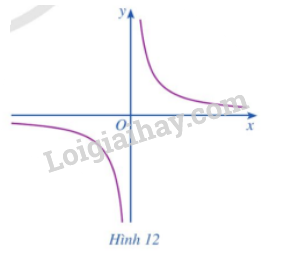
Cho hàm số \(y = f\left( x \right) = \frac{1}{x}\) có đồ thị là đường cong như Hình 12. Tìm \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)\)
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = - \infty \).
LT2
Trả lời câu hỏi Luyện tập 2 trang 23 SGK Toán 12 Cánh diều
Tìm tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + 3x}}{{x - 5}}\).
Phương pháp giải:
Đường thẳng \(x = {x_o}\) được gọi là đường tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
\(\mathop {\lim }\limits_{x \to x_o^ - } f\left( x \right) = + \infty \) ,\(\mathop {\lim }\limits_{x \to x_o^ - } f\left( x \right) = - \infty \),\(\mathop {\lim }\limits_{x \to x_o^ + } f\left( x \right) = + \infty \),\(\mathop {\lim }\limits_{x \to x_o^ + } f\left( x \right) = - \infty \).
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\backslash \left\{ 5 \right\}\).
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {5^ - }} y = \mathop {\lim }\limits_{x \to {5^ - }} \frac{{{x^2} + 3x}}{{x - 5}} = - \infty \\\mathop {\lim }\limits_{x \to {5^ + }} y = \mathop {\lim }\limits_{x \to {5^ + }} \frac{{{x^2} + 3x}}{{x - 5}} = + \infty \end{array} \right.\)
Vậy đường thẳng \(x = 5\) là tiệm cận đứng của đồ thị hàm số đã cho