Giải mục 2 trang 69, 70, 71 SGK Toán 12 tập 2 - Cánh diều
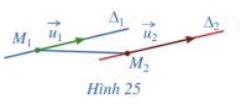
Cho hai đường thẳng phân biệt \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({M_1},{M_2}\) và tương ứng có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) . a) Giả sử \({\Delta _1}\) song song với \({\Delta _2}\) (Hình 25). Các cặp vectơ sau có cùng phương hay không: \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \); \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \)?
HĐ5
Trả lời câu hỏi Hoạt động 5 trang 69 SGK Toán 12 Cánh diều
Cho hai đường thẳng phân biệt \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({M_1},{M_2}\) và tương ứng có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) .
a) Giả sử \({\Delta _1}\) song song với \({\Delta _2}\) ( Hình 25 ). Các cặp vectơ sau có cùng phương hay không: \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \); \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \)?
b) Giả sử \({\Delta _1}\) và \({\Delta _2}\) cắt nhau ( Hình 26 ). Hai vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) có cùng phương hay không? Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) có đồng phẳng hay không?

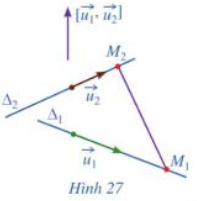
c) Giả sử \({\Delta _1}\) và \({\Delta _2}\) chéo nhau ( Hình 27 ). Hai vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) có cùng phương hay không? Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) có đồng phẳng hay không?
Phương pháp giải:
+ Sử dụng kiến thức về giá của vectơ trong không gian để trả lời: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ.
+ Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để trả lời: Cho đường thẳng \(\Delta \) và vectơ \(\overrightarrow u \) khác \(\overrightarrow 0 \) . Vectơ \(\overrightarrow u \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).
Lời giải chi tiết:
a) Vì \({\Delta _1}\) song song với \({\Delta _2}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) cùng phương.
Vì \({M_1}\) thuộc đường thẳng \({\Delta _1}\), \({M_2}\) thuộc đường thẳng \({\Delta _2}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \) không cùng phương.
b) Vì \({\Delta _1}\) và \({\Delta _2}\) cắt nhau nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) đồng phẳng.
c) Vì \({\Delta _1}\) và \({\Delta _2}\) chéo nhau nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) không đồng phẳng.
LT5
Trả lời câu hỏi Luyện tập 5 trang 70 SGK Toán 12 Cánh diều
Bằng cách giải hệ phương trình, xác định vị trí tương đối của hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = {t_1}\\y = 1\\z = 0\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 2\\y = {t_2}\\z = 0\end{array} \right.\).
Phương pháp giải:
Sử dụng cách giải hệ phương trình chứa hai phương trình của hai đường thẳng, ta xác định vị trí tương đối của hai đường thẳng.
Lời giải chi tiết:
Xét hệ phương trình: \(\left\{ \begin{array}{l}{t_1} = 2\\1 = {t_2}\\0 = 0\end{array} \right.\). Hệ phương trình này có một nghiệm duy nhất nên hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.