Giải mục 2 trang 83, 84 SGK Toán 10 tập 1 - Chân trời sáng tạo — Không quảng cáo

HĐ Khám phá 2

Bạn có nhận xét gì về giá của các cặp vectơ$\overrightarrow {AB}$ và $\overrightarrow {CD}$, $\overrightarrow {PQ}$ và $\overrightarrow {RS}$ trong Hình 6?

Lời giải chi tiết:

Ta có:  giá của $\overrightarrow {AB}$ là đường thẳng AB, giá của $\overrightarrow {CD}$là đường thẳng CD, và thấy rằng 2 đường thẳng này trùng nhau suy ra giá của 2 vecto này trùng nhau.

Tương tự ta thấy giá của cặp $\overrightarrow {PQ}$ và $\overrightarrow {RS}$ song song với nhau.

Thực hành 3

Quan sát Hình 8 và gọi tên các vectơ:

a) Cùng phương với vectơ $\overrightarrow x$;

b) Cùng hướng với vectơ $\overrightarrow a$ ;

Ngược hướng với vectơ  $\overrightarrow u$.

Phương pháp giải:

a) Xác định các vectơ có giá song song hoặc trùng với giá của vectơ x

b) Xác định các vectơ cùng phương, cùng chiều với vectơ a

c) Xác định các vectơ cùng phương, ngược chiều với vectơ u

Lời giải chi tiết:

a) Ta có:

Giá của vectơ $\overrightarrow {\rm{w}}$ trùng với giá của $\overrightarrow x$

Giá của vectơ $\overrightarrow y$, $\overrightarrow z$song song với giá của $\overrightarrow x$

Suy ra các vectơ cùng phương với vectơ $\overrightarrow x$ là $\overrightarrow {\rm{w}}$, $\overrightarrow y$và $\overrightarrow z$

b) Ta có:

Vectơ $\overrightarrow b$ có giá song song với vectơ $\overrightarrow a$và có cùng hướng từ trên xuống với vectơ $\overrightarrow a$nên vectơ $\overrightarrow b$ cùng hướng với vectơ $\overrightarrow a$

c) Ta có:

Vectơ $\overrightarrow v$ có giá song song với vectơ $\overrightarrow u$và ngược hướng từ dưới lên trên so với vectơ $\overrightarrow u$nên vectơ $\overrightarrow v$ ngược hướng với vectơ $\overrightarrow u$

Thực hành 4

Khẳng định sau đây đúng hay sai? Hãy giải thích.

Nếu 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ  $\overrightarrow {AB}$ và $\overrightarrow {AC}$cùng hướng.

Phương pháp giải:

Thay đổi các vị trí của 3 điểm, kiểm tra hai vectơ $\overrightarrow {AB}$  và $\overrightarrow {AC}$ có cùng hướng hay không.

Lời giải chi tiết:

Khẳng định trên sai. Vì khi 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ  $\overrightarrow {AB}$ và $\overrightarrow {AC}$ cùng phương nhưng chưa chắc là cùng hướng.

Chẳng hạn:

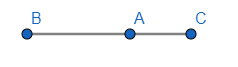
Khi A nằm giữa B và C thì hướng của vectơ  $\overrightarrow {AB}$ là từ phải sang trái, còn hướng của vectơ  $\overrightarrow {AC}$là từ trái sang phải nên hai vectơ này là ngược hướng.