Giải mục 2 trang 75, 76, 77 SGK Toán 10 tập 1 - Chân trời sáng tạo — Không quảng cáo

Vận dụng 1

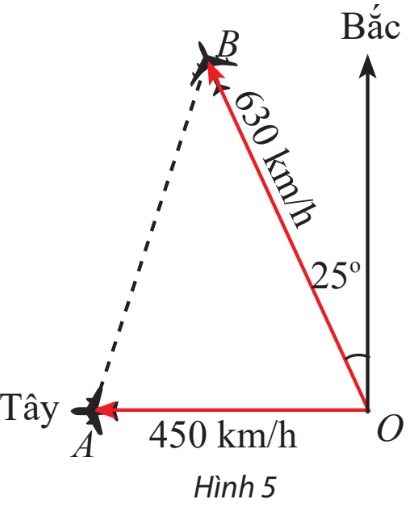
Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với tốc độ 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc \({25^o}\) về phía tây với tốc độ 630 km/h (Hình 5). Sau 90 phút, hai máy bay cách nhau bao nhiêu kilomet? Giả sử chúng đang ở cùng độ cao.

Phương pháp giải:

Bước 1. Tính góc \(\widehat {BOA} = {90^o} - {25^o}.\)

Bước 2: Áp dụng định lí cosin: \(A{B^2} = O{A^2} + O{B^2} - 2OA.OB\cos O\)

Lời giải chi tiết:

Ta có: \(\widehat {BOA} = {90^o} - {25^o} = {65^o}.\)

Sau 90 phút = 1,5 giờ:

Máy bay thứ nhất đi được quãng đường (OA) là: \(450.1,5 = 675\;(km)\)

Máy bay thứ hai đi được quãng đường (OB) là: \(630.1,5 = 945\;(km)\)

Áp dụng định lí cosin trong tam giác OAB, ta có:

\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2OA.OB\cos O\\ \Leftrightarrow A{B^2} = {675^2} + {945^2} - 2.675.945\cos {65^o}\\ \Rightarrow AB \approx 900\end{array}\)

Vậy sau 90 phút, hai máy bay cách nhau khoảng 900 km.

Vận dụng 2

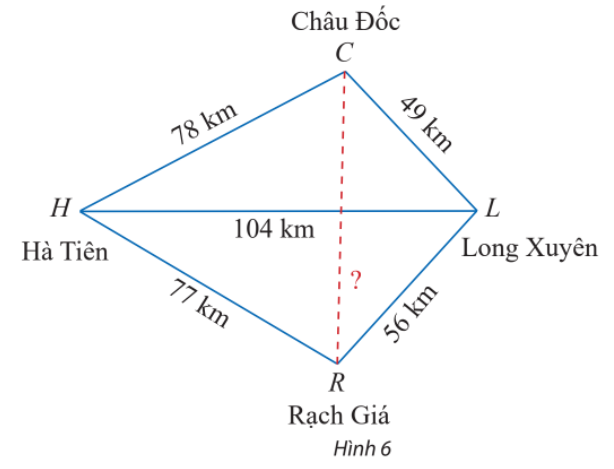
Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên. Dựa theo các khoảng cách đã cho trên Hình 6, tính khoảng cách giữa Châu Đốc và Rạch Giá.

Phương pháp giải:

Bước 1: Áp dụng hệ quả của định lí cosin để tính các góc \(\widehat {CHL},\;\widehat {LHR}\)\(\cos \;\widehat {CHL} = \frac{{C{H^2} + H{L^2} - C{L^2}}}{{2.CH.HL}};\cos \;\widehat {LHR} = \frac{{H{L^2} + H{R^2} - R{L^2}}}{{2.HL.HR}}\)

Bước 2: Áp dụng định lí cosin \(C{R^2} = H{C^2} + H{R^2} - 2.HC.HR\cos \widehat {CHR}\)

Lời giải chi tiết:

Bước 1: Áp dụng hệ quả của định lí cosin trong tam giác HCL, ta có:\(\begin{array}{l}\cos \;\widehat {CHL} = \frac{{C{H^2} + H{L^2} - C{L^2}}}{{2.CH.HL}} = \frac{{{{78}^2} + {{104}^2} - {{49}^2}}}{{2.78.104}} = \frac{{4833}}{{5408}}\\ \Rightarrow \;\widehat {CHL} \approx {26^o}39'40,05''\end{array}\)

Áp dụng hệ quả của định lí cosin trong tam giác HLR, ta có:\(\begin{array}{l}\cos \;\widehat {LHR} = \frac{{H{L^2} + H{R^2} - L{R^2}}}{{2.HL.HR}} = \frac{{{{104}^2} + {{77}^2} - {{56}^2}}}{{2.104.77}} = \frac{{13609}}{{16016}}\\ \Rightarrow \;\widehat {LHR} \approx {31^o}49'10,4''\\ \Rightarrow \;\widehat {CHR} \approx {58^o}28'50,45''\end{array}\)

Bước 2: Áp dụng định lí cosin \(C{R^2} = H{C^2} + H{R^2} - 2.HC.HR\cos \widehat {CHR}\)

\(\begin{array}{l} \Leftrightarrow C{R^2} = {78^2} + {77^2} - 2.78.77\cos {58^o}28'50,45''\\ \Rightarrow CR \approx 75,72\end{array}\)

Vậy khoảng cách giữa Châu Đốc và Rạch Giá là 75, 72 km.