Giải mục 2 trang 62, 63 SGK Toán 10 tập 1 - Chân trời sáng tạo — Không quảng cáo

HĐ Khám phá 2

Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc \(\widehat {xOM}\) và \(\widehat {xON}.\)

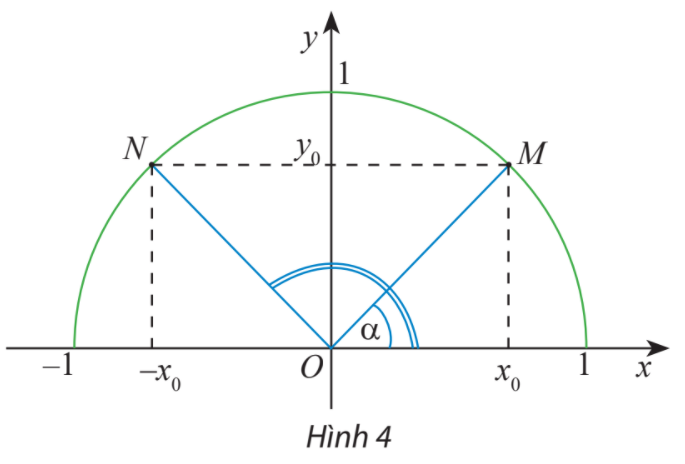
Phương pháp giải:

Tính góc \(\widehat {xON}\) theo góc \(\widehat {xOM}.\)

Lời giải chi tiết:

Gọi H là hình chiếu vuông góc của N Ox.

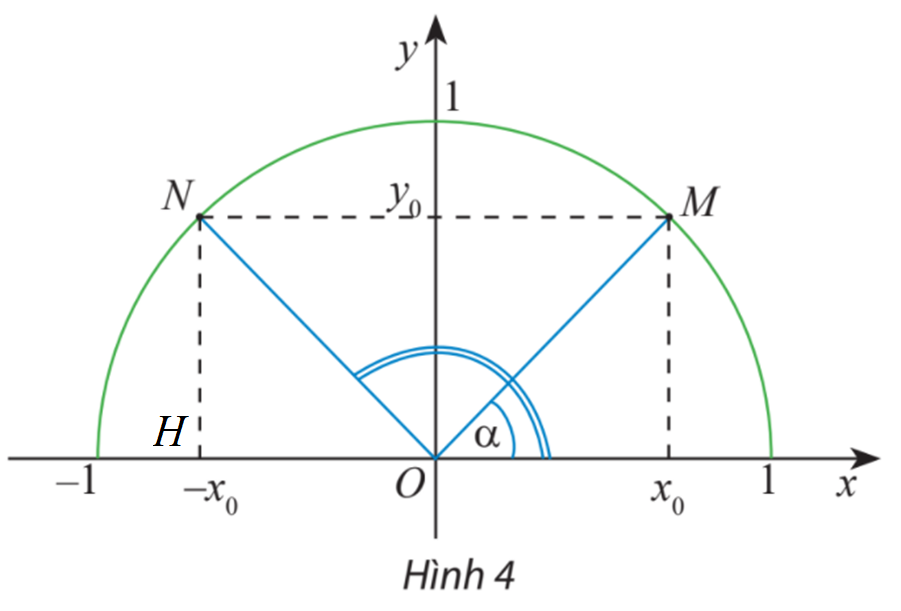
Ta có: \(\widehat {NOH} = \widehat {ONM} = \widehat {OMN} = \widehat {MOx} = \alpha \) (do NM song song với Ox)

Mà \(\widehat {xOM} + \widehat {NOH} = {180^o}\)

Suy ra \(\widehat {xON} + \widehat {MOx} = {180^o}\)

Thực hành 2

Tính các giá trị lượng giác: \(\sin {120^o};\cos {150^o};\cot {135^o}.\)

Phương pháp giải:

\(\begin{array}{l}\sin {120^o} = \sin \;({180^o} - {60^o});\\\cos {150^o} =  - \cos \;({180^o} - {30^o});\\\cot {135^o} =  - \cot \;({180^o} - {45^o}).\end{array}\)

Lời giải chi tiết:

\(\begin{array}{l}\sin {120^o} = \sin \;({180^o} - {60^o}) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\cos {150^o} =  - \cos \;({180^o} - {30^o}) =  - \cos {30^o} =  - \frac{{\sqrt 3 }}{2};\\\cot {135^o} =  - \cot \;({180^o} - {45^o}) =  - \cot {45^o} =  - 1.\end{array}\)

Vận dụng 1

Cho biết \(\sin \alpha  = \frac{1}{2},\) tìm góc \(\alpha \;({0^o} \le \alpha  \le {180^o})\) bằng cách vẽ nửa đường tròn đơn vị.

Phương pháp giải:

Vẽ nửa đường tròn đơn vị.

\(\sin \alpha  = \frac{1}{2}\) nên lấy các điểm có tung độ là \(\frac{1}{2}\). Từ đó tính góc \(\alpha \).

Lời giải chi tiết:

Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho: \(\widehat {xOM} = \alpha \)

Do \(\sin \alpha  = \frac{1}{2}\) nên tung độ của M bằng \(\frac{1}{2}.\)

Vậy ta xác định được hai điểm N và M thỏa mãn \(\sin \widehat {xON} = \sin \widehat {xOM} = \frac{1}{2}\)

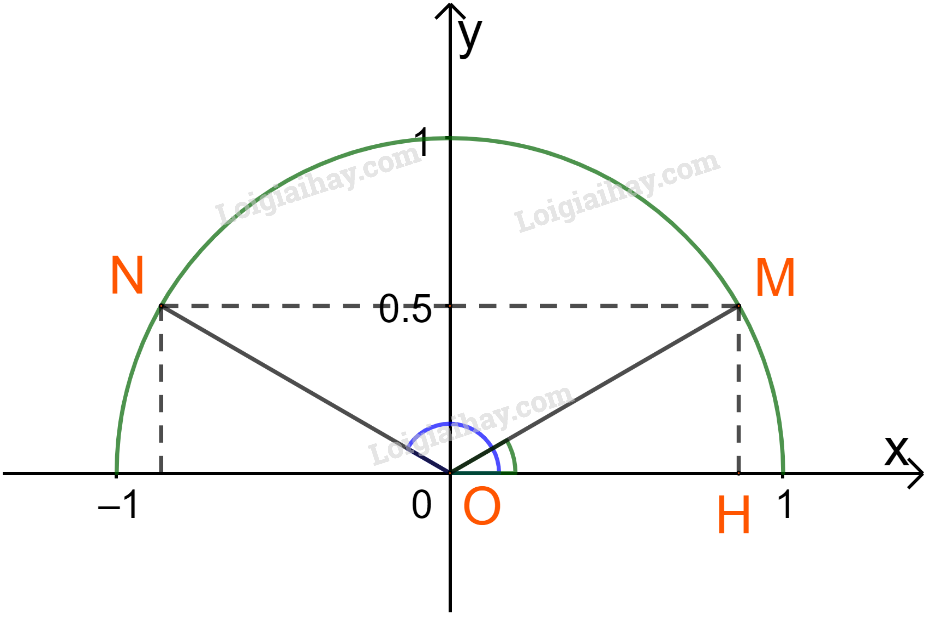
Đặt \(\beta  = \widehat {xOM} \Rightarrow \widehat {xON} = {180^o} - \beta \)

Xét tam giác OHM vuông tại H ta có: \(MH = \frac{1}{2} = \frac{{OM}}{2} \Rightarrow \beta  = {30^o}\)

\( \Rightarrow \widehat {xON} = {180^o} - {30^o} = {150^o}\)

Vậy \(\alpha  = {30^o}\) hoặc \(\alpha  = {150^o}\)