Giải mục 2 trang 9, 10 SGK Toán 11 tập 1 - Chân trời sáng tạo
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9).
Hoạt động 3
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9). Đo và cho biết \(\widehat {AOB}\) có số đo bằng bao nhiêu độ.
Phương pháp giải:
Vẽ đường tròn và xác định góc như phía trên đã học
Lời giải chi tiết:
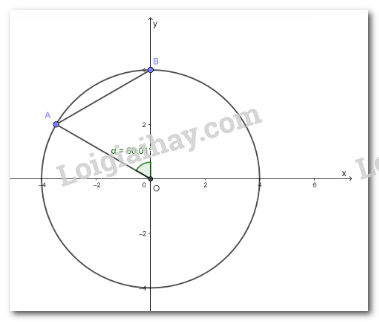
\( \Rightarrow \widehat {AOB} = 60^\circ \)
Thực hành 2
Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:
|
Số đo theo độ |
0° |
? |
45° |
60° |
? |
120° |
? |
150° |
180° |
|
Số đo theo rad |
? |
\(\frac{\pi }{6}(rad)\) |
? |
? |
\(\frac{\pi }{2}(rad)\) |
? |
\(\frac{{3\pi }}{4}(rad)\) |
? |
\(\pi (rad)\) |
Phương pháp giải:
Sử dụng công thức \({\alpha ^ \circ } = \frac{{\pi \alpha }}{{180}}\,\)rad ; \(\alpha \,\,rad = {\left( {\frac{{180\alpha }}{\pi }} \right)^0}\)
Lời giải chi tiết:
|
Số đo theo độ |
0° |
30° |
45° |
60° |
90° |
120° |
135° |
150° |
180° |
|
Số đo theo rad |
0 |
\(\frac{\pi }{6}(rad)\) |
\(\frac{\pi }{4}\left( {rad} \right)\) |
\(\frac{\pi }{3}\left( {rad} \right)\) |
\(\frac{\pi }{2}(rad)\) |
\[\frac{{2\pi }}{3}(rad)\] |
\(\frac{{3\pi }}{4}(rad)\) |
\(\frac{{5\pi }}{6}(rad)\) |
\(\pi (rad)\) |