Giải mục 3 trang 24, 25, 26 SGK Toán 12 tập 1 - Cánh diều — Không quảng cáo

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 24 SGK Toán 12 Cánh diều

Cho hàm số $y = f\left( x \right) = x + 1 + \frac{1}{{x - 1}}$ có đồ thị $\left( C \right)$ và đường thẳng $y = x + 1$ (Hình 15). Tìm $\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right];\mathop {\lim }\limits_{x \to  - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right]$

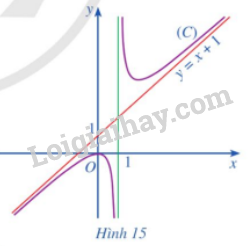
Phương pháp giải:

Quan sát đồ thị

Lời giải chi tiết:

Ta có: $\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to  + \infty } \frac{1}{{x - 1}} = 0\\\mathop {\lim }\limits_{x \to  - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to  - \infty } \frac{1}{{x - 1}} = 0\end{array} \right.$

LT3

Trả lời câu hỏi Luyện tập 3 trang 25 SGK Toán 12 Cánh diều

Chứng minh rằng đường thẳng $y =  - x$ là tiệm cận xiên của đồ thị hàm số $y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}$.

Phương pháp giải:

Đưởng thẳng $y = ax + b\left( {a \ne 0} \right)$ được gọi là tiệm cận xiên của đồ thị hàm số $y = f\left( x \right)$ nếu:

$\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0$ hoặc $\mathop {\lim }\limits_{x \to  - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0$.

Lời giải chi tiết:

Ta có: $y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}} =  - x + \frac{3}{{x + 2}}$.

Xét $\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( { - x} \right)} \right] = \mathop {\lim }\limits_{x \to  + \infty } \frac{3}{{x + 2}} = 0$.

Vậy đường thẳng $y =  - x$ là đường tiệm cận xiên của đồ thị hàm số $y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}$

LT4

Trả lời câu hỏi Luyện tập 4 trang 26 SGK Toán 12 Cánh diều

Tìm tiệm cận xiên của đồ thị hàm số $y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}$.

Phương pháp giải:

Đưởng thẳng $y = ax + b\left( {a \ne 0} \right)$ được gọi là tiệm cận xiên của đồ thị hàm số $y = f\left( x \right)$ nếu:

$\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0$ hoặc $\mathop {\lim }\limits_{x \to  - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0$.

Lời giải chi tiết:

Ta có: $y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}} = x - 6 + \frac{{20}}{{x + 3}}$.

Xét $\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( {x - 6} \right)} \right] = \mathop {\lim }\limits_{x \to  + \infty } \frac{{20}}{{x + 3}} = 0$.

Vậy đường thẳng $y = x - 6$ là đường tiệm cận xiên của đồ thị hàm số $y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}$