Giải mục 3 trang 54,55,56 SGK Toán 12 tập 2 - Cánh diều — Không quảng cáo

HĐ5

Trả lời câu hỏi Hoạt động 5 trang 54 SGK Toán 12 Cánh diều

Cho mặt phẳng (P) đi qua điểm $I({x_0};{y_0};{z_0})$ có $\overrightarrow n (A;B;C)$ là vecto pháp tuyến. Giả sử M(x;y;z) là một điểm bất kì thuộc mặt phẳng (P) (Hình 9)

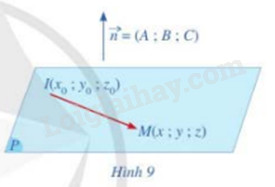
a) Tính tích vô hướng $\overrightarrow n .\overrightarrow {IM}$

b) Hãy biểu diễn $\overrightarrow n .\overrightarrow {IM}$ theo ${x_0},{y_0},{z_0};x,y,z$ và A, B, C

Phương pháp giải:

Sử dụng công thức biểu thức tọa độ của tích vô hướng

Lời giải chi tiết:

a) $\overrightarrow {IM}  = (x - {x_0};y - {y_0};z - {z_0})$

$\overrightarrow n .\overrightarrow {IM}  = A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0})$

b) $\overrightarrow n .\overrightarrow {IM}  = A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = Ax + By + Cz - A{x_0} - B{y_0} - C{z_0}$

HĐ6

Trả lời câu hỏi Hoạt động 6 trang 55 SGK Toán 12 Cánh diều

Cho mặt phẳng (P) đi qua điểm I(1;3;-2) có cặp vecto chỉ phương là $\overrightarrow u  = (1;1;3),\overrightarrow v  = (2; - 1;2)$ (Hình 10)

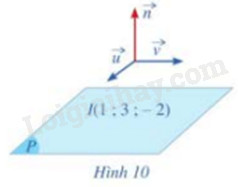
a) Hãy chỉ ra một vecto pháp tuyến $\overrightarrow n$ của mặt phẳng (P)

b) Lập phương trình mặt phẳng (P) đi qua điểm I(1;3;-2) biết vecto pháp tuyển $\overrightarrow n$

Phương pháp giải:

a) Nếu hai vecto $\overrightarrow u  = ({x_1};{y_1};{z_1})$ và $\overrightarrow v  = ({x_2};{y_2};{z_2})$ là cặp vecto chỉ phương của mặt phẳng (P) thì $\overrightarrow n  = [\overrightarrow u ;\overrightarrow v ] = \left( {\left| \begin{array}{l}{y_1}\;\;\;\;{z_1}\;\\{y_2}\;\;\;\;{z_2}\end{array} \right|;\left| \begin{array}{l}{z_1}\;\;\;\;{x_1}\\{x_2}\;\;\;\;{z_1}\end{array} \right|;\left| \begin{array}{l}{x_1}\;\;\;\;{y_1}\\{x_2}\;\;\;\;{y_2}\end{array} \right|} \right)$ là một vecto pháp tuyến của mặt phẳng (P)

b) Mặt phẳng (P) đi qua điểm $I({x_0};{y_0};{z_0})$ và nhận $\overrightarrow n  = (A;B;C)$ làm vecto pháp tuyến có phương trình là $A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0$

Lời giải chi tiết:

a) Vecto pháp tuyến của mặt phẳng (P) là $\overrightarrow n  = [\overrightarrow u ;\overrightarrow v ] = (5; - 4;3)$

b) Phương trình mặt phẳng (P): $5(x - 1) - 4(y - 3) + 3(z + 2) = 0 \Leftrightarrow 5x - 4y + 3z + 13 = 0$

HĐ7

Trả lời câu hỏi Hoạt động 7 trang 55 SGK Toán 12 Cánh diều

Cho ba điểm H(-1;1;2), I(1;3;2), K(-1;4;5) cùng thuộc mặt phẳng (P) (Hình 11)

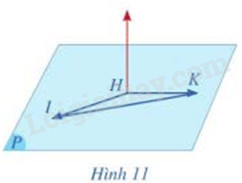
a) Tím tọa độ của các vecto $\overrightarrow {HI} ,\overrightarrow {HK}$. Từ đó hãy chứng tỏ rằng ba điểm H, I, K không thẳng hàng

b) Lập phương trình mặt phẳng (P) đi qua điểm H(-1;1;2), biết cặp vecto chỉ phương là $\overrightarrow {HI} ,\overrightarrow {HK}$

Phương pháp giải:

a) $A({a_1};{a_2};{a_3}),B({b_1};{b_2};{b_3}) \Rightarrow \overrightarrow {AB}  = ({b_1} - {a_1};{b_2} - {a_2};{b_3} - {a_3})$

b) Tìm vecto pháp tuyến của mặt phẳng $\overrightarrow n  = (A;B;C)$. Mặt phẳng (P) đi qua điểm $I({x_0};{y_0};{z_0})$ và nhận $\overrightarrow n  = (A;B;C)$ làm vecto pháp tuyến có phương trình là $A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0$

Lời giải chi tiết:

a) $\overrightarrow {HI}  = (2;2;0),\overrightarrow {HK}  = (0;3;3)$

Có $\overrightarrow {HI}  \ne k.\overrightarrow {HK}$ suy ra H, I, K không thẳng hàng

b) Vecto pháp tuyến của mặt phẳng (P) là: $\overrightarrow n  = [\overrightarrow {HI} ;\overrightarrow {HK} ] = (6; - 6;6)$

Phương trình mặt phẳng (P) là: $6(x + 1) - 6(y - 1) + 6(z - 2) = 0 \Leftrightarrow 6x - 6y + 6z = 0 \Leftrightarrow x - y + z = 0$