Giải mục 4 trang 57,58,59 SGK Toán 12 tập 2 - Cánh diều — Không quảng cáo

HĐ8

Trả lời câu hỏi Hoạt động 8 trang 57 SGK Toán 12 Cánh diều

Cho mặt phẳng $({P_1}):2x + 2y + 2z + 1 = 0$ (1) và mặt phẳng $({P_2}):x + y + z - 1 = 0$ (2).

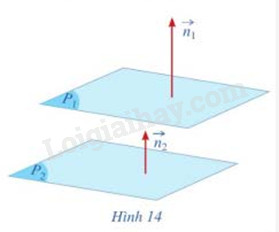
a) Gọi $\overrightarrow {{n_1}}  = (2;2;2),\overrightarrow {{n_2}}  = (1;1;1)$ lần lượt là vecto pháp tuyến của hai mặt phẳng $({P_1}),({P_2})$ (Hình 14). Tìm liên hệ giữa $\overrightarrow {{n_1}}$ và $2\overrightarrow {{n_2}}$

b) Tìm các hệ số tự do ${D_1},{D_2}$ lần lượt trong hai phương trình (1), (2). So sánh ${D_1}$ và $2{D_2}$

c) Nêu vị trí tương đối của hai mặt phẳng $({P_1}),({P_2})$

Phương pháp giải:

a), (b) Xác định $\overrightarrow {{n_1}}$ và $2\overrightarrow {{n_2}}$, ${D_1}$ và $2{D_2}$ rồi so sánh

b) Quan sát hình vẽ

Lời giải chi tiết:

a) $\;\overrightarrow {{n_1}}  = 2\overrightarrow {{n_2}}  = (2;2;2)$

b) ${D_1}$= 1; $2{D_2}$ = -2

Vậy ${D_1} \ne 2{D_2}$

c) $({P_1})//({P_2})$

HĐ9

Trả lời câu hỏi Hoạt động 9 trang 58 SGK Toán 12 Cánh diều

Cho mặt phẳng $({P_1})$ có phương trình tổng quát là $x + 2y + z + 1 = 0$ và mặt phẳng $({P_2})$ có phương trình tổng quát là $3x - 2y + z + 5 = 0$

Gọi $\overrightarrow {{n_1}}  = (1;2;1),\overrightarrow {{n_2}}  = (3; - 2;1)$ lần lượt là vecto pháp tuyến của hai mặt phẳng $({P_1}),({P_2})$ (Hình 14). Hai vecto  $\overrightarrow {{n_1}}$,$\overrightarrow {{n_2}}$ có vuông góc với nhau hay không?

Phương pháp giải:

$\overrightarrow {{n_1}}  \bot \overrightarrow {{n_2}}  \Leftrightarrow \overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 0$

Lời giải chi tiết:

$\overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 1.3 + 2.( - 2) + 1.1 = 0$ suy ra $\overrightarrow {{n_1}}$,$\overrightarrow {{n_2}}$ vuông góc với nhau