Giải mục 5 trang 37 SGK Toán 11 tập 1 - Kết nối tri thức
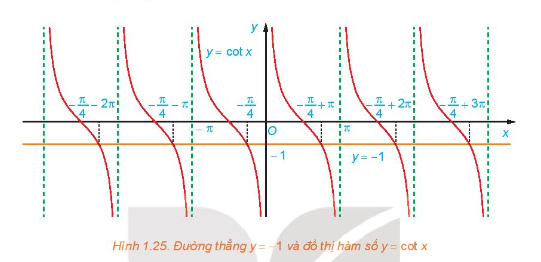
a) Quan sát Hình 1.25, hãy cho biết đường thẳng (y = - 1) cắt đồ thị hàm số (y = cot x) tại mấy điểm trên khoảng (left( {0;pi } right)?)
HĐ 5
a) Quan sát Hình 1.25, hãy cho biết đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = \cot x\) tại mấy điểm trên khoảng \(\left( {0;\pi } \right)?\)
 b) Dựa vào tính tuần hoàn của hàm cotang, hãy viết công thức nghiệm của phương trình đã cho.
b) Dựa vào tính tuần hoàn của hàm cotang, hãy viết công thức nghiệm của phương trình đã cho.
Phương pháp giải:
Nghiệm của phương trình \(\cot x = - 1\) là hoành độ các giao điểm của đường thẳng \(y = - 1\) và đồ thị hàm số \(y = \cot x\)
Lời giải chi tiết:
a) Từ Hình 1.25, ta thấy đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = \cot x\;\)tại 1 điểm \(x = - \frac{\pi }{4} + \pi \) trên khoảng \(\left( {0;\pi } \right)\)
b) Ta có công thức nghiệm của phương trình là: \(x = - \frac{\pi }{4} + \pi + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
LT5
Giải các phương trình sau:
a) \(\cot x = 1;\) b) \(\sqrt 3 \cot x + 1 = 0\)
Phương pháp giải:
Sử dụng công thức nghiệm \(\cot x = m\; \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \;\;\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết:
a) \(\cot x = 1\; \Leftrightarrow \cot x = \cot \frac{\pi }{4}\;\;\; \Leftrightarrow x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
b) \(\sqrt 3 \cot x + 1 = 0\;\;\; \Leftrightarrow \sqrt 3 \cot x = - 1\; \Leftrightarrow \cot x = - \frac{{\sqrt 3 }}{3}\;\; \Leftrightarrow \cot x = \cot \left( { - \frac{\pi }{3}} \right)\)
\( \Leftrightarrow x = - \frac{\pi }{3} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)