Giải mục II trang 50, 51 SGK Toán 10 tập 1 - Cánh diều — Không quảng cáo

Hoạt động 2

a) Lập bảng xét dấu của tam thức bậc hai $f\left( x \right) = {x^2} - x - 2$

b) Giải bất phương trình ${x^2} - x - 2 > 0$

Phương pháp giải:

a) Tìm nghiệm của phương trình ${x^2} - x - 2 = 0$, xét hệ số và lập bảng xét dấu.

b) Dựa vào bảng xét dấu, lấy các khoảng để $f\left( x \right) > 0$

Lời giải chi tiết:

a) Ta có tam thức bậc hai $f\left( x \right) = {x^2} - x - 2$ có 2 nghiệm phân biệt ${x_1} =  - 1,{x_2} = 2$ và hệ số $a = 1 > 0$

Ta có bảng xét dấu f(x) như sau:

Vậy tập nghiệm của bất phương trình là $\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)$b) Từ bảng xét dấu ta thấy $f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x <  - 1\\x > 2\end{array} \right.$

Luyện tập – vận dụng 2

Giải các bất phương trình bậc hai sau:

a) $3{x^2} - 2x + 4 \le 0$

b) $- {x^2} + 6x - 9 \ge 0$

Phương pháp giải:

Giải bất phương trình dạng $f\left( x \right) > 0$.

Bước 1: Xác định dấu của hệ số a và tìm nghiệm của $f\left( x \right)$(nếu có)

Bước 2: Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho $f\left( x \right)$ mang dấu “+”

Bước 3: Các bất phương trình bậc hai có dạng $f\left( x \right) < 0,f\left( x \right) \ge 0,f\left( x \right) \le 0$ được giải bằng cách tương tự.

Lời giải chi tiết:

a) Ta có $a = 3 > 0$ và tam thức bậc hai $f\left( x \right) = 3{x^2} - 2x + 4$ có $\Delta ' = {1^2} - 3.4 =  - 11 < 0$

=> $f\left( x \right) = 3{x^2} - 2x + 4$ vô nghiệm.

=> $3{x^2} - 2x + 4 > 0\forall x \in \mathbb{R}$

b) Ta có: $a =  - 1 < 0$ và $\Delta ' = {3^2} - \left( { - 1} \right).\left( { - 9} \right) = 0$

=> $f\left( x \right) =  - {x^2} + 6x - 9$ có nghiệm duy nhất $x = 3$.

=> $- {x^2} + 6x - 9 < 0\forall x \in \mathbb{R}\backslash \left\{ 3 \right\}$

Hoạt động 3

Cho bất phương trình ${x^2} - 4x + 3 > 0\left( 2 \right)$.

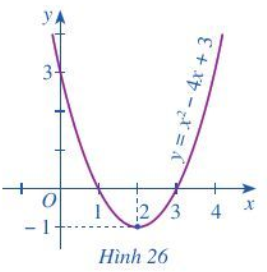
Quan sát parabol $\left( P \right):{x^2} - 4x + 3$ ở Hình 26 và cho biết:

a) Bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía nào của trục hoành.

b) Phần parabol (P) nằm phía trên trục hoành ứng với những giá trị nào của x.

Phương pháp giải:

- Nếu dấu bất phương trình dương thì bất phương trình biểu diễn phần (P) phía trên trục hoành và ngược lại.

Lời giải chi tiết:

a) Từ đồ thị ta thấy bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía trên trục hoành.

b) Phần parabol (P) nằm phía trên trục hoành ứng với các giá trị của x thuộc $\left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)$

Luyện tập – vận dụng 3

Giải mỗi bất phương trình bậc hai sau bằng cách sử dụng đồ thị:

a) ${x^2} + 2x + 2 > 0$

b) $- 3{x^2} + 2x - 1 > 0$

Phương pháp giải:

Bước 1: Vẽ đồ thị biểu diễn các hàm số.

Bước 2: Quan sát đồ thị và lấy các giá trị tương ứng với bất phương trình.

Lời giải chi tiết:

a) Ta có đồ thị:

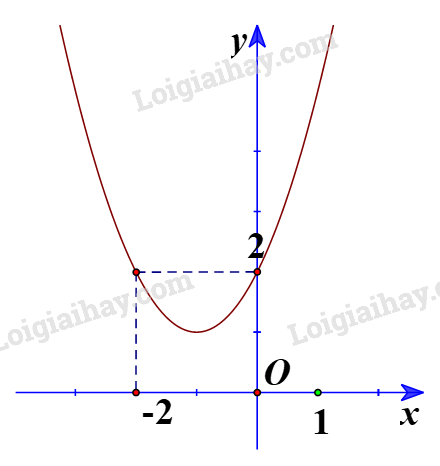
Từ đồ thị ta thấy ${x^2} + 2x + 2 > 0$ biểu diễn phần parabol $y = {x^2} + 2x + 2$ nằm phía trên trục hoành, tương ứng với mọi $x \in \mathbb{R}$.

Vậy tập nghiệm của bất phương trình ${x^2} + 2x + 2 > 0$ là $\mathbb{R}$.

b) Ta có đồ thị:

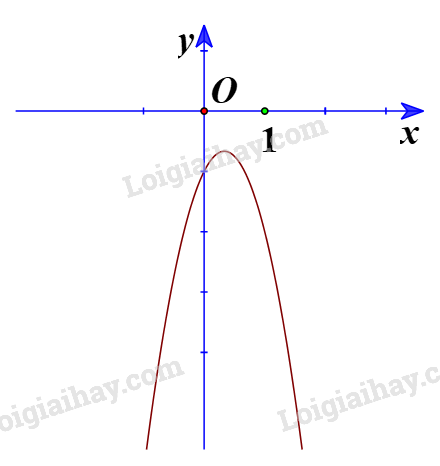
Từ đồ thị ta thấy $- 3{x^2} + 2x - 1 > 0$ biểu diễn phần parabol $y =  - 3{x^2} + 2x - 1$ nằm phía trên trục hoành, tương ứng với $x \in \emptyset$

Vậy tập nghiệm của bất phương trình $- 3{x^2} + 2x - 1 > 0$ là $\emptyset$.