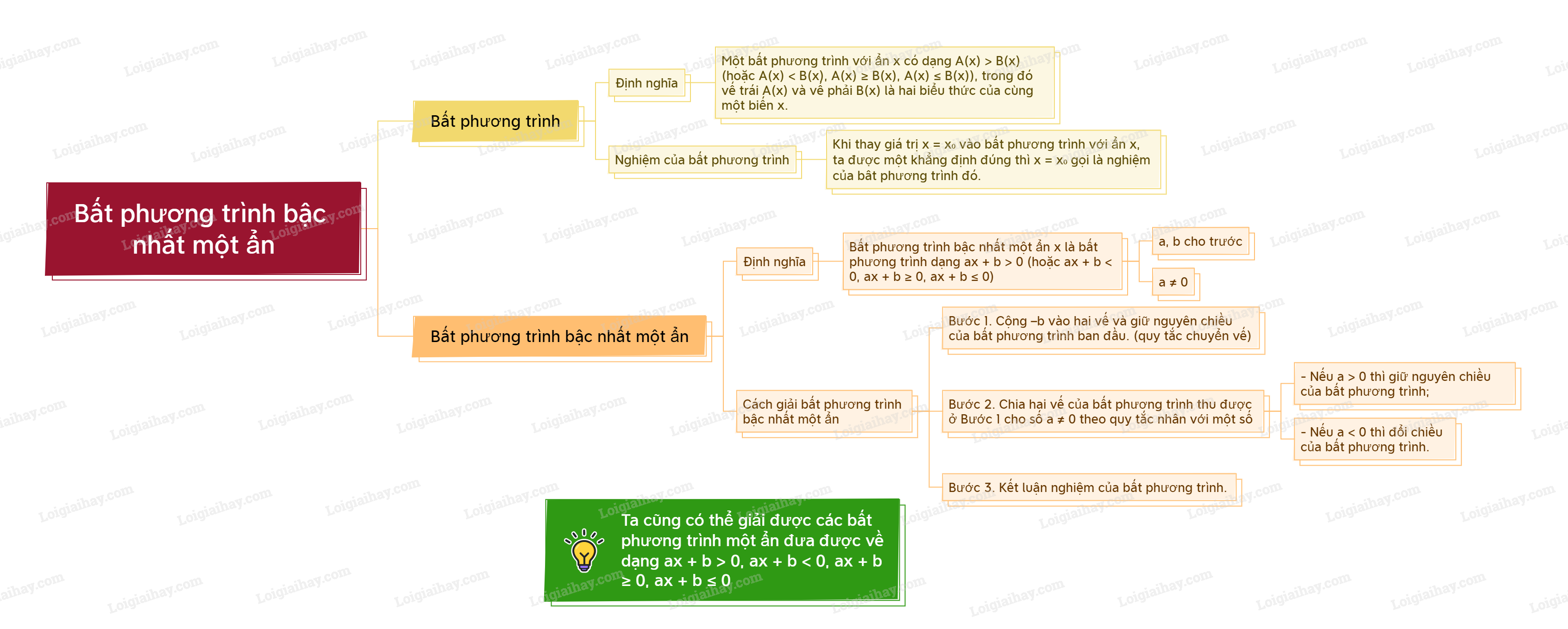
Lý thuyết Bất phương trình bậc nhất một ẩn Toán 9 Cùng khám phá
1. Mở đầu về bất phương trình Định nghĩa bất phương trình Cho A(x), B(x) là hai biểu thức của biến x. Khi cần tìm x sao cho A(x) > B(x) (hoặc A(x) < B(x), A(x) ( & ge ) B(x), A(x) ( le ) B(x)) thì ta nói cho A(x) > B(x) (hoặc A(x) < B(x), A(x) ( & ge ) B(x), A(x) ( le ) B(x)) là một bất phương trình ẩn x. A(x) và B(x) lần lượt được gọi là vế trái và vế phải của bất phương trình.
1. Mở đầu về bất phương trình
Định nghĩa bất phương trình
|
Cho A(x), B(x) là hai biểu thức của biến x. Khi cần tìm x sao cho A(x) > B(x) (hoặc A(x) < B(x), A(x) \( \ge \) B(x), A(x) \( \le \) B(x)) thì ta nói cho A(x) > B(x) (hoặc A(x) < B(x), A(x) \( \ge \) B(x), A(x) \( \le \) B(x)) là một bất phương trình ẩn x. A(x) và B(x) lần lượt được gọi là vế trái và vế phải của bất phương trình. |
Nghiệm của bất phương trình
|
Khi thay giá trị \(x = {x_0}\) vào hai vế của một bất phương trình ẩn x mà được một khẳng định đúng thì ta nói \(x = {x_0}\) (hay \({x_0}\)) là một nghiệm của bất phương trình đó. |
Ví dụ:
Số -2 là nghiệm của bất phương trình \(2x - 10 < 0\) vì \(2.\left( { - 2} \right) - 10 = - 4 - 10 = - 14 < 0\).
Số 6 không là nghiệm của bất phương trình \(2x - 10 < 0\) vì \(2.6 - 10 = 12 - 10 = 2 > 0\).
2. Bất phương trình bậc nhất một ẩn
Định nghĩa
|
Bất phương trình dạng \(ax + b > 0\) (hoặc \(ax + b < 0,ax + b \ge 0,ax + b \le 0\)), trong đó a, b là hai số đã cho, \(a \ne 0\) được gọi là bất phương trình bậc nhất một ẩn (x là ẩn). |
Ví dụ: \(3x + 16 \le 0\); \( - 3x > 0\) là các bất phương trình bậc nhất một ẩn x.
\({x^2} - 4 \ge 0\) không phải là một bất phương trình bậc nhất một ẩn x vì \({x^2} - 4\) là một đa thức bậc hai.
\(3x - 2y < 2\) không phải là một bất phương trình bậc nhất một ẩn vì đa thức \(3x - 2y\) là đa thức với hai biến x và y.
3. Cách giải bất phương trình bậc nhất một ẩn
Giải một bất phương trình nghĩa là tìm tất cả các nghiệm của nó.
|
Để giải bất phương trình \(ax + b > 0\) (hoặc \(ax + b < 0,ax + b \ge 0,ax + b \le 0\)), trong đó \(a \ne 0\), ta thực hiện ba bước sau: Bước 1. Cộng –b vào hai vế và giữ nguyên chiều của bất phương trình ban đầu. Bước 2. Chia hai vế của bất phương trình thu được ở Bước 1 cho số \(a \ne 0\) theo quy tắc: - Nếu \(a > 0\) thì giữ nguyên chiều của bất phương trình; - Nếu \(a < 0\) thì đổi chiều của bất phương trình. Bước 3. Kết luận nghiệm của bất phương trình. |
Ví dụ: Giải bất phương trình \( - 2x - 4 > 0\)
Lời giải: Ta có:
\(\begin{array}{l} - 2x - 4 > 0\\ - 2x > 0 + 4\\ - 2x > 4\\x < 4.\left( { - \frac{1}{2}} \right)\\x < - 2\end{array}\)
Vậy nghiệm của bất phương trình là \(x < - 2\).
Lưu ý:
Ở Bước 1, ta đã thực hiện quy tắc sau, gọi là quy tắc chuyển vế: Khi chuyển một hạng tử từ vế này sang vế kia, ta phải đổi dấu hạng tử đó.
Quy tắc thực hiện ở Bước 2 gọi là quy tắc nhân với một số: Khi nhân hai vế của một bất phương trình cùng một số khác 0, ta phải:
- Giữ nguyên chiều bất phương trình nếu số đó dương;
- Đổi chiều bất phương trình nếu số đó âm.
Nhờ hai quy tắc này, ta có thể giải được nhiều bất phương trình phức tạp hơn.