Lý thuyết diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
a) Diện tích xung quanh.
a) Diện tích xung quanh
1. Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
a) Định nghĩa
- Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích bốn mặt bên của hình hộp chữ nhật.
- Diện tích toàn phần của hình hộp chữ nhật là tổng của diện tích xung quanh và diện tích hai đáy.
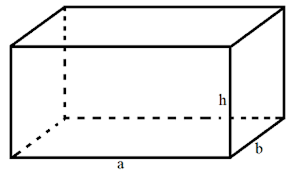
b) Quy tắc: Giử sử hình hộp chữ nhật có chiều dài là \(a\), chiều rộng là \(b\) và chiều cao là \(h\).
- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng đơn vị đo).
\({S_{xq}} = (a + b) \times 2 \times h\)
- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
\({S_{tp}} = S{}_{xq} + \,\,{S_{day}} \times 2 = (a + b) \times 2 \times h + 2 \times a \times b\)
Lưu ý:
- Chu vi mặt đáy bằng tổng của chiều dài và chiều rộng nhân với \(2\).
- Diện tích mặt đáy bằng tích của chiều dài và chiều rộng.
Ví dụ: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài \(8cm\), chiều rộng \(6cm\) và chiều cao \(4cm\).
Giải:
Chu vi đáy của hình hộp chữ nhật là:
\((8 + 6) \times 2 = 28\;(cm)\)
Diện tích xung quanh của hình hộp chữ nhật đó là:
\(28 \times 4 = 112\;(c{m^2})\)
Diện tích một đáy là:
\(8 \times 6 = 48\;(c{m^2})\)
Diện tích toàn phần của hình hộp chữ nhật đó là:
\(112 + 48 \times 2 = 208\;(c{m^2})\)
Đáp số: Diện tích xung quanh: \(112c{m^2}\);
Diện tích toàn phần: \(208c{m^2}\).
Chú ý: Khi tìm diện tích xung quanh ta có thể làm gộp thành :\((8 + 6) \times 2 \times 4 = 112c{m^2}\) .