Lý thuyết cộng hai số thập phân — Không quảng cáo

a) Ví dụ 1: Đường gấp khúc ABC có đoạn thẳng AB dài \(1,84m\) và đoạn thẳng BC dài \(2,45m\). Hỏi đường gấp khúc đó dài bao nhiêu mét?

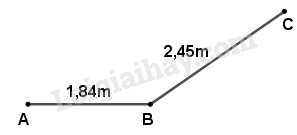
Ta phải thực hiện phép cộng:

\(1,84 + 2,45 = ? \;(m)\)

Ta có:    \(1,84m = 184 cm\)

\(2,45m = 145 cm\)

\(\begin{array}{l}\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{184\,\,\,\,\,\,\,\,\,\,}\\{245\,\,\,\,\,\,\,\,\,\,}\end{array}}\\\hline{\,\,\,\,\;\;\,429\,\,(cm)}\end{array}\\429cm = 4,29m\end{array}\)

Vậy:     \(1,84 + 2,45 = 4,29 \;(m)\).

Thông thường ta đặt tính rồi làm như sau:

\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{1,84\,\,\,\,\,\,\,\,\,\,}\\{2,45\,\,\,\,\,\,\,\,\,\,}\end{array}}\\\hline{\,\,\,\,\;4,29\,\,(m)}\end{array}\)

• Thực hiện phép cộng như cộng số tự nhiên.

• Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng

b) Ví dụ 2: \(15,9 + 8,75 = ?\)

Ta đặt tính rồi làm như sau:

\(\begin{array}{*{20}{c}}{ + \,\,\begin{array}{*{20}{c}}{15,9\,\,\,\,\,}\\{8,75}\end{array}}\\\hline{\,\,\;\,24,65}\end{array}\)

• Thực hiện phép cộng như cộng số tự nhiên.

• Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.

Muốn  cộng hai số thập phân ta làm như sau:

- Viết số hạng này dưới số hạng kia làm sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.

- Cộng như cộng các số tự nhiên.

- Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.