Lý thuyết chia số thập phân cho một số thập phân
a) Ví dụ 1: Một thanh sắt dài 6,2dm
a) Ví dụ 1: Một thanh sắt dài \(6,2dm\) cân nặng \(23,56 kg\). Hỏi \(1dm\) của thanh sắt đó cân nặng bao nhiêu ki-lô-gam?
Ta phải thực hiện phép chia: \(23,56 : 6,2 = \;?\;\)
Ta có: \(23,56 : 6,2 = (23,56 \times 10) : (6,2 \times 10)\)
\(23,56 : 6,2 = 235,6 : 62\)
Thông thường ta đặt tính rồi làm như sau:
• Phần thập phân của số \(6,2\) có một chữ số.
• Chuyển dấu phẩy của số \(23,56\) sang bên phải một chữ số được \(235,6\); bỏ dấu phẩy ở số \(6,2\) được \(62\).
+) Thực hiện phép chia \(235,6 : 62\).
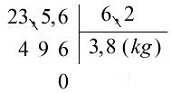
Vậy: \( 23,56 : 6,2 = 3,8\; (kg)\)
b) Ví dụ 2: \(82,55 : 1,27 = \;?\)
Ta đặt tính rồi làm như sau:
• Phần thập phân của hai số \(82,55\) và \(1,27\) cùng có hai chữ số; bỏ dấu phẩy ở hai số đó được \(8255\) và \(127\).
• Thực hiện phép chia \(8255 : 127\).
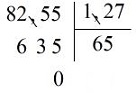
Muốn chia một số thập phân cho một số thập phân ta làm như sau:
- Đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì chuyển dấu phẩy ở số bị chia sang bên phải bấy nhiêu chữ số.
- Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như chia số tự nhiên.