Lý thuyết chia một số thập phân cho một số tự nhiên
a) Ví dụ 1: Một sợi dây dài 8,4m được chia thành 4
a) Ví dụ 1: Một sợi dây dài \(8,4m\) được chia thành \(4\) đoạn bằng nhau. Hỏi mỗi đoạn dây dài bao nhiêu mét?
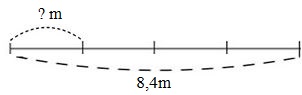
Ta phải thực hiện phép chia: \(8,4 : 4 = \;?\;(m)\)
Ta có: \(8,4 m = 84dm\)
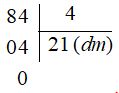
\(21dm=2,1m\)
Vậy: \(8,4 : 4 = 2,1 \;(m)\).
Thông thường ta đặt tính rồi làm như sau:
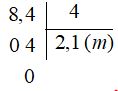
• \(8\) chia \(4\) được \(2\), viết \(2\); \(2\) nhân \(4\) bằng \(8\); \(8\) trừ \(8\) bằng \(0\), viết \(0\).
• Viết dấu phẩy vào bên phải \(2\).
• Hạ \(4\); \( 4\) chia \(4\) được \(1\), viết \(1\);
\(1\) nhân \(4\) bằng \(4\); \(4\) trừ \(4\) bằng \( 0\), viết \(0\).
b) Ví dụ 2: \(72,58 : 19 =\; ?\)
Ta đặt tính rồi làm tương tự như ví dụ 1:
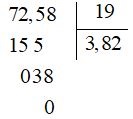
Muốn chia một số thập phân với một số tự nhiên ta làm như sau:
- Chia phần nguyên của số bị chia cho số chia.
- Viết dấu phẩy vào bên phải thương đã tìm trước khi lấy chữ số đầu tiên ở phần thập phân của số bị chia để tiếp tục thực hiện phép chia.
- Tiếp tục chia với từng chữ số ở phần thập phân của số bị chia.