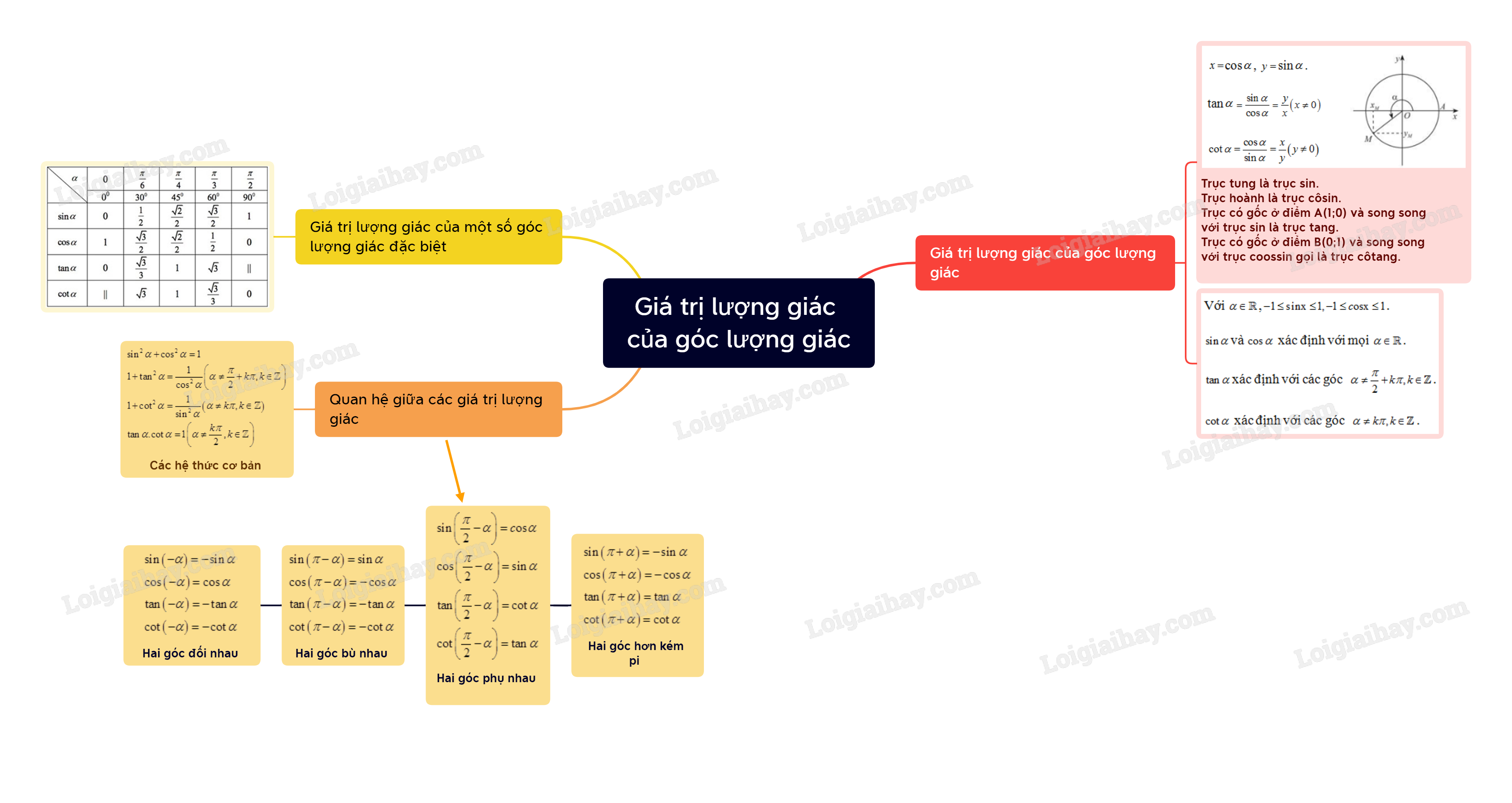
Lý thuyết Giá trị lượng giác của một góc lượng giác - SGK Toán 11 Chân trời sáng tạo
1. Giá trị lượng giác của góc lượng giác
1. Giá trị lượng giác của góc lượng giác
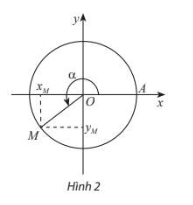
- Trên đường tròn, lấy điểm M(x;y) như hình vẽ. Khi đó:
\(x = \)cos\(\alpha \), \(y = \)sin\(\alpha \).
tan\(\alpha \)\( = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{y}{x}\left( {x \ne 0} \right)\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{x}{y}\left( {y \ne 0} \right)\)
- Các giá trị sin\(\alpha \), cos\(\alpha \), tan\(\alpha \), cot\(\alpha \) được gọi là các giá trị lượng giác của góc lượng giác \(\alpha \).
*Chú ý:
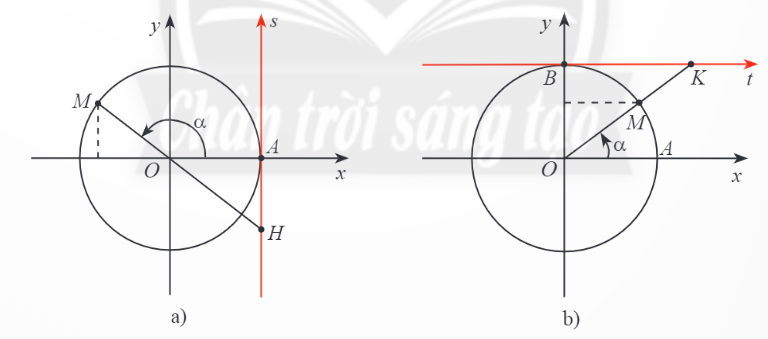
a, Trục tung là trục sin, trục hoành là trục côsin.
Trục As có gốc ở điểm A(1;0) và song song với trục sin là trục tang.
Trục Bt có gốc ở điểm B(0;1) và song song với trục coossin gọi là trục côtang.
b, \(\sin \alpha \)và \(\cos \alpha \) xác định với mọi \(\alpha \in \mathbb{R}\).
\(\tan \alpha \)xác định với các góc \(\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
\(\cot \alpha \) xác định với các góc \(\alpha \ne k\pi ,k \in \mathbb{Z}\).
c, Với mọi góc lượng giác \(\alpha \) và số nguyên k, ta có:
\(\begin{array}{l}\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \\\cos \left( {\alpha + k2\pi } \right) = \cos \alpha \\\tan \left( {\alpha + k\pi } \right) = \tan \alpha \\\cot \left( {\alpha + k\pi } \right) = \cot \alpha \end{array}\)
d, Bảng các giá trị lượng giác đặc biệt
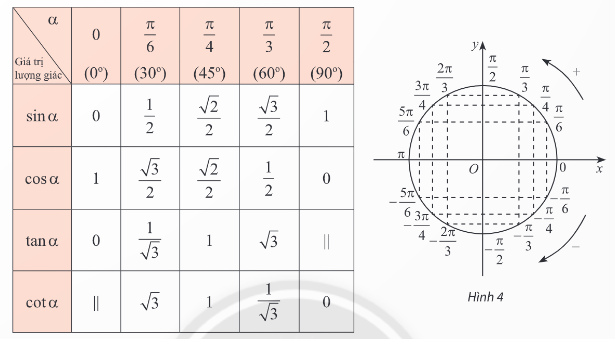
2. Tính giá trị lượng giác của một góc bằng máy tính cầm tay
- Lần lượt ấn các phím SHIFT \( \to \)MENU \( \to \)2:
Để chọn đơn vị độ: ấn phím 1 (Degree).
Để chọn đơn vị radian: ấn phím 2 (Radian).
- Ấn các phím MENU 1 để vào chế độ tính toán.
3. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\left( {\alpha \ne k\pi ,k \in \mathbb{Z}} \right)\\\tan \alpha .\cot \alpha = 1\left( {\alpha \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\end{array}\)
4. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt
- Hai góc đối nhau \(\alpha \)và \( - \alpha \)
\(\begin{array}{l}\sin \left( { - \alpha } \right) = - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \\\tan \left( { - \alpha } \right) = - \tan \alpha \\\cot \left( { - \alpha } \right) = - \cot \alpha \end{array}\)
- Hai góc bù nhau (\(\alpha \)và \(\pi \)-\(\alpha \))
\(\begin{array}{l}\sin \left( {\pi - \alpha } \right) = \sin \alpha \\\cos \left( {\pi - \alpha } \right) = - \cos \alpha \\\tan \left( {\pi - \alpha } \right) = - \tan \alpha \\\cot \left( {\pi - \alpha } \right) = - \cot \alpha \end{array}\)
- Hai góc phụ nhau (\(\alpha \)và \(\frac{\pi }{2}\)-\(\alpha \))
\(\begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \\\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array}\)
- Hai góc hơn kém \(\pi \)(và \(\pi \)+\(\alpha \))
\(\begin{array}{l}\sin \left( {\pi + \alpha } \right) = - \sin \alpha \\\cos \left( {\pi + \alpha } \right) = - \cos \alpha \\\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array}\)