Lý thuyết Giới hạn của dãy số - SGK Toán 11 Chân trời sáng tạo — Không quảng cáo

1, Giới hạn hữu hạn của dãy số

a, Giới hạn 0 của dãy số

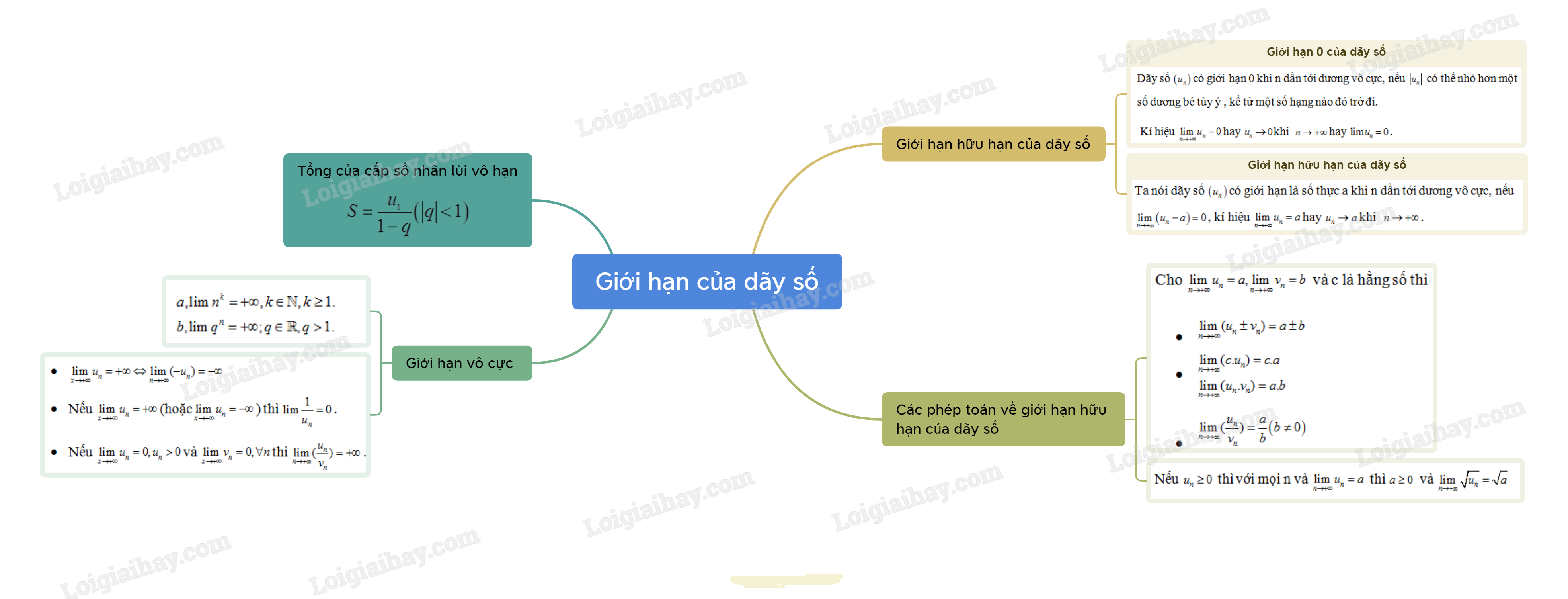
- Dãy số $\left( {{u_n}} \right)$ có giới hạn 0 khi n dần tới dương vô cực, nếu $\left| {{u_n}} \right|$ có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi.

Kí hiệu $\mathop {\lim }\limits_{n \to  + \infty } {u_n} = 0$ hay ${u_n} \to 0$khi  $n \to  + \infty$ hay $\lim {u_n} = 0$.

* Chú ý:

+ $\lim \frac{1}{{{n^k}}} = 0,k \in \mathbb{Z}.$

+ Nếu $\left| q \right| < 1$ thì $\lim {q^n} = 0$

b, Giới hạn hữu hạn của dãy số

Ta nói dãy số $\left( {{u_n}} \right)$ có giới hạn là số thực a khi n dần tới dương vô cực, nếu $\mathop {\lim }\limits_{n \to  + \infty } \left( {{u_n} - a} \right) = 0$, kí hiệu $\mathop {\lim }\limits_{n \to  + \infty } {u_n} = a$ hay ${u_n} \to a$ khi  $n \to  + \infty$.

* Chú ý: Nếu ${u_n} = c$(c là hằng số) thì $\mathop {\lim }\limits_{n \to  + \infty } {u_n} = c$

2. Các phép toán về giới hạn hữu hạn của dãy số

Cho $\mathop {\lim }\limits_{n \to  + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to  + \infty } {v_n} = b$ và c là hằng số thì

• $\mathop {\lim }\limits_{n \to  + \infty } ({u_n} \pm {v_n}) = a \pm b$
• $\begin{array}{l}\mathop {\lim }\limits_{n \to  + \infty } (c.{u_n}) = c.a\\\mathop {\lim }\limits_{n \to  + \infty } ({u_n}.{v_n}) = a.b\end{array}$
• $\mathop {\lim }\limits_{n \to  + \infty } (\frac{{{u_n}}}{{{v_n}}}) = \frac{a}{b}\left( {b \ne 0} \right)$
• Nếu ${u_n} \ge 0$ thì với mọi n và $\mathop {\lim }\limits_{n \to  + \infty } {u_n} = a$ thì $a \ge 0$ và $\mathop {\lim }\limits_{n \to  + \infty } \sqrt {{u_n}}  = \sqrt a$

3. Tổng của cấp số nhân lùi vô hạn

Cấp số nhân $\left( {{u_n}} \right)$ có công bội q thỏa mãn $\left| q \right| < 1$ được gọi là cấp số nhân lùi vô hạn.

Tổng của cấp số nhân lùi vô hạn là:

$S = \frac{{{u_1}}}{{1 - q}}\left( {\left| q \right| < 1} \right)$

4. Giới hạn vô cực

- Dãy số $\left( {{u_n}} \right)$được gọi là có giới hạn $+ \infty$khi $n \to  + \infty$nếu ${u_n}$ có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu $\mathop {\lim }\limits_{x \to  + \infty } {u_n} =  + \infty$ hay ${u_n} \to  + \infty$ khi $n \to  + \infty$.

- Dãy số $\left( {{u_n}} \right)$ được gọi là có giới hạn $- \infty$khi $n \to  + \infty$ nếu $\mathop {\lim }\limits_{x \to  + \infty } \left( { - {u_n}} \right) =  + \infty$, kí hiệu $\mathop {\lim }\limits_{x \to  + \infty } {u_n} =  - \infty$ hay ${u_n} \to  - \infty$ khi $n \to  + \infty$.

* Chú ý:

• $\mathop {\lim }\limits_{x \to  + \infty } {u_n} =  + \infty  \Leftrightarrow \mathop {\lim }\limits_{n \to  + \infty } ( - {u_n}) =  - \infty$
• Nếu $\mathop {\lim }\limits_{x \to  + \infty } {u_n} =  + \infty$(hoặc$\mathop {\lim }\limits_{x \to  + \infty } {u_n} =  - \infty$) thì $\lim \frac{1}{{{u_n}}} = 0$.
• Nếu $\mathop {\lim }\limits_{x \to  + \infty } {u_n} = 0,{u_n} > 0$và $\mathop {\lim }\limits_{x \to  + \infty } {v_n} = 0,\forall n$thì $\mathop {\lim }\limits_{n \to  + \infty } (\frac{{{u_n}}}{{{v_n}}}) =  + \infty$.

*Nhận xét:

$\begin{array}{l}a,\lim {n^k} =  + \infty ,k \in \mathbb{N},k \ge 1.\\b,\lim {q^n} =  + \infty ;q \in \mathbb{R},q > 1.\end{array}$