Lý thuyết Giá trị lượng giác của một góc từ 0 đến 180. Định lí cosin và định lí sin trong tam giác - SGK Toán 10 Cánh diều
I. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180 II. ĐỊNH LÍ COSIN III. ĐỊNH LÍ SIN
I. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180
1. G iá trị lượng giác của một góc từ 0 đến 180
+) Với mỗi góc \(\alpha ({0^o} \le \alpha {\rm{\;}} \le {180^o})\) có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị để \(\widehat {xOM} = \alpha .\)Khi đó:
\(\sin \alpha {\rm{\;}} = {y_0}\) là tung độ của M
\(\cos \alpha {\rm{\;}} = {x_0}\) là hoành độ của M
\(\tan \alpha {\rm{\;}} = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha {\rm{\;}} \ne {90^o})\)
\(\cot \alpha {\rm{\;}} = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha {\rm{\;}} \ne {0^o},\alpha {\rm{\;}} \ne {180^o})\)
2. Q uan hệ giữa các giá trị lượng giác của hai góc bù nha u
|
Hai góc bù nhau, \(\alpha \) và \({180^o} - \alpha \) : \(\begin{array}{*{20}{l}}{\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha }\\{\cos \left( {{{180}^o} - \alpha } \right) = {\rm{\;}} - \cos \alpha }\\{\tan \left( {{{180}^o} - \alpha } \right) = {\rm{\;}} - \tan \alpha (\alpha {\rm{\;}} \ne {{90}^o})}\\{\cot \left( {{{180}^o} - \alpha } \right) = {\rm{\;}} - \cot \alpha ({0^o} < \alpha {\rm{\;}} < {{180}^o})}\end{array}\) |
Hai góc phụ nhau, \(\alpha \) và \({90^o} - \alpha \) : \(\begin{array}{*{20}{l}}{\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha }\\{\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha }\\{\tan \left( {{{90}^o} - \alpha } \right) = \cot \alpha (\alpha {\rm{\;}} \ne {{90}^o},{0^o} < \alpha {\rm{\;}} < {{180}^o})}\\{\cot \left( {{{90}^o} - \alpha } \right) = \tan \alpha (\alpha {\rm{\;}} \ne {{90}^o},{0^o} < \alpha {\rm{\;}} < {{180}^o})}\end{array}\) |
3. C ác giá trị lượng giác của một số góc đặc biệt
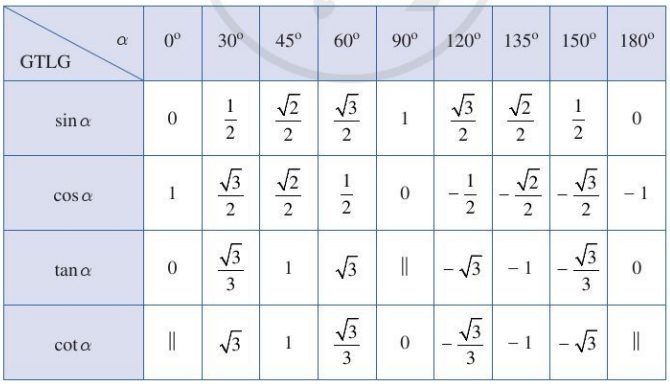
II . ĐỊNH LÍ COSIN
1. Định lí cosin
Trong tam giác ABC:
\(\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} - 2bc\cos A}\\{{b^2} = {c^2} + {a^2} - 2ca\cos B}\\{{c^2} = {a^2} + {b^2} - 2ab\cos C}\end{array}\)
2. Hệ quả
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)
III . ĐỊNH LÍ SIN
1. Định lí sin
Trong tam giác ABC: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\)
(R là bán kính đường tròn ngoại tiếp tam giác ABC)
2. Hệ quả
Hệ quả
\(a = 2R.\sin A;\quad b = 2R\sin B;\quad c = 2R\sin C\)
\(\sin A = \frac{a}{{2R}};\quad \sin B = \frac{b}{{2R}};\quad \sin C = \frac{c}{{2R}}.\)