Lý thuyết Hai đường thẳng song song trong không gian - SGK Toán 11 Cánh Diều — Không quảng cáo

I. Vị trí tương đối của hai đường thẳng

Cho hai đường thẳng a, b phân biệt trong không gian. Khi đó chỉ xảy ra các trường hợp sau:

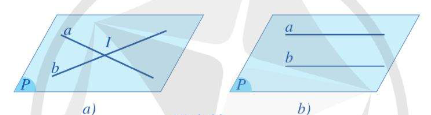
• Có một mặt phẳng chứa a và b. Khi đó ta nói a và b đồng phẳng. Khi đó, a và b có thể cắt nhau, song song với nhau hoặc trùng nhau.

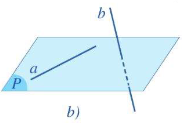
• Không có mặt phẳng nào chứa a và b. Khi đó ta nói a và b chéo nhau.

* Nhận xét: Hai đường thẳng song song là hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung. Kí hiệu //.

II. Tính chất của hai đường thẳng song song

• Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.

• Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì 3 giao tuyến đó đồng quy hoặc đôi một song song.

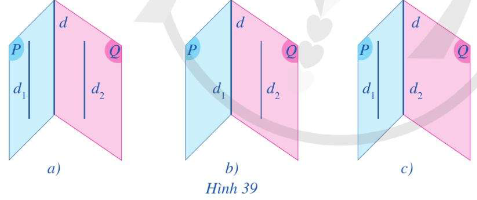
* Hệ quả: Nếu hai mặt phẳng chứa 2 đường thẳng song song với nhau thì giao tuyến (nếu có) của chúng song song với 2 đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

• Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì song song với nhau.