Lý thuyết Hai mặt phẳng song song - SGK Toán 11 Cánh Diều
I. Hai mặt phẳng song song
I. Hai mặt phẳng song song
Hai mặt \(\left( P \right)\) và \(\left( Q \right)\) được gọi là song song với nhau nếu chúng không có điểm chung. Kí hiệu\(\left( P \right)\)// \(\left( Q \right)\) hay \(\left( Q \right)\)//\(\left( P \right)\).
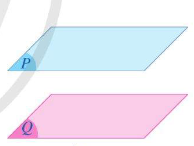
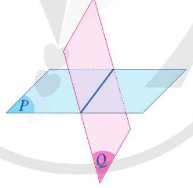
*Nhận xét: Hai mặt \(\left( P \right)\) và \(\left( Q \right)\) có diểm chung. Khi đó, chúng cắt nhau theo một đường thẳng.
II. Điều kiện và tính chất
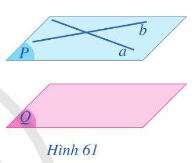
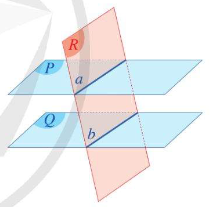
- Nếu mặt phẳng \(\left( P \right)\) chứa hai đường thẳng cắt nhau a,b và a,b cùng song song với mặt phẳng phẳng \(\left( Q \right)\)thì \(\left( P \right)\)song song với \(\left( Q \right)\)
- Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
* Hệ quả:
- Nếu đường thẳng a song song với mặt phẳng \(\left( Q \right)\) thì có duy nhất một mặt phẳng chứa a và song song với mặt phẳng \(\left( Q \right)\)
- Nếu 2 mặt phẳng phân biệt cùng song song với mặt phẳng thứ 3 thì song song với nhau.
- Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song. Nếu mặt phẳng \(\left( R \right)\) cắt mặt phẳng \(\left( P \right)\)thì cũng cắt mặt phẳng \(\left( Q \right)\)và hai giao tuyến song song với nhau.
III. Định lí Thalès
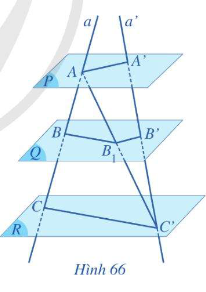
Nếu a, b là hai cát tuyến bất kì cắt 3 mặt phẳng song song \(\left( P \right)\) , \(\left( Q \right)\)và\(\left( R \right)\) lần lượt tại các điểm A, B, C và A’, B’, C’ thì
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\)