Lý thuyết Hàm số bậc nhất y = ax + b (a ≠ 0) SGK Toán 8 - Chân trời sáng tạo
Hàm số bậc nhất là gì?
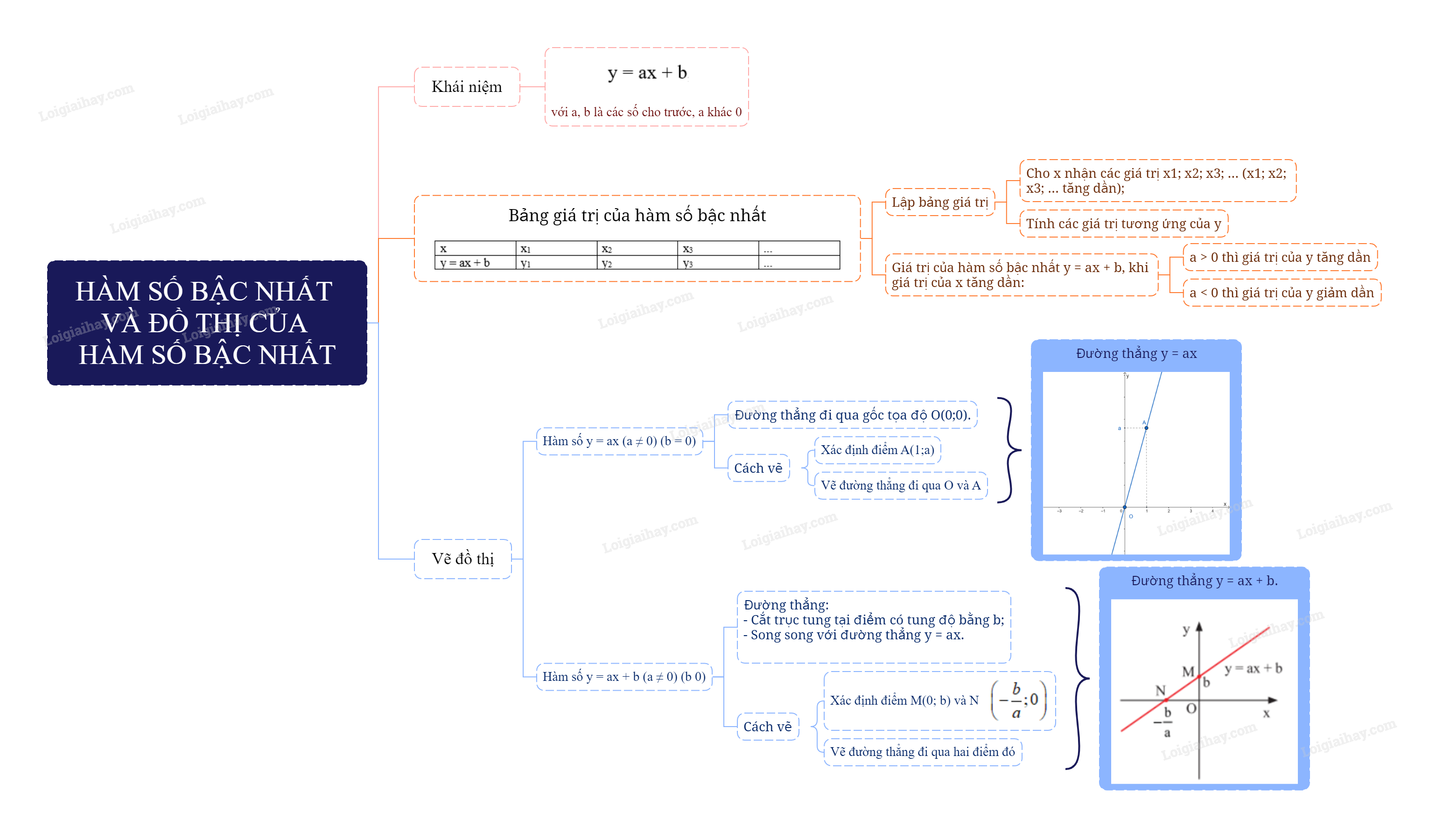
1. Hàm số bậc nhất
Khái niệm:
Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b với a, b là các số cho trước và a khác 0.
Ví dụ: y = 2x – 3 là hàm số bậc nhất với a = 2 và b = -3
y = x + 4 là hàm số bậc nhất với a = 1, b = 4
2. Bảng giá trị của hàm số bậc nhất
Để lập bảng giá trị của hàm số bậc nhất y = ax + b ta lần lượt cho x nhận các giá trị x 1 ; x 2 ; x 3 ; ... (x 1 ; x 2 ; x 3 ; ... tăng dần) và tính các giá trị tương ứng của y rồi ghi vào bảng có dạng như sau:
|
x |
x 1 |
x 2 |
x 3 |
... |
|
y = ax + b |
y 1 |
y 2 |
y 3 |
... |
Chú ý: Trong bảng giá trị của hàm số bậc nhất y = ax + b, khi giá trị của x tăng dần:
- Nếu a > 0 thì giá trị của y tăng dần.
- Nếu a < 0 thì giá trị của y giảm dần.
Ví dụ: Bảng giá trị của hàm số bậc nhất y = f(x) = 5x + 3 với x lần lượt bằng -2; -1; 0; 1; 2 là:
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y = ax + b |
-7 |
-2 |
3 |
8 |
13 |
3. Vẽ đồ thị của hàm số bậc nhất
Hàm số y = ax (a \( \ne \) 0 , b = 0)
Đồ thị của hàm số y = ax (a \( \ne \) 0) là một đường thẳng đi qua gốc tọa độ O(0;0) .
Cách vẽ:
Bước 1. Xác định một điểm M trên đồ thị khác gốc tọa độ O, chẳng hạn M(1; a)
Bước 2. Vẽ đường thẳng đi qua hai điểm O và M.
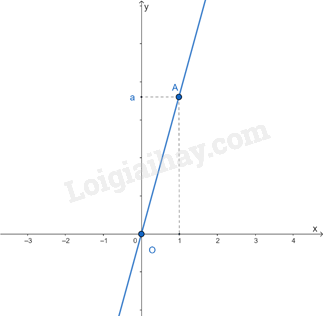
Chú ý: Đồ thị của hàm số y = ax còn được gọi là đường thẳng y = ax.
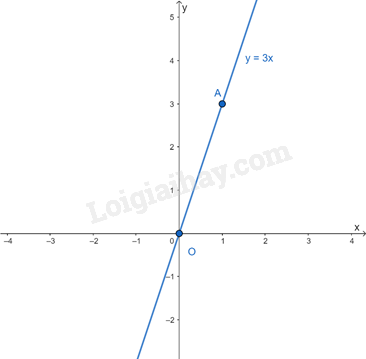
Ví dụ: Cho hàm số y = 3x.
Cho x = 1 ta có y = 3. Ta vẽ điểm A(1; 3)
Đồ thị hàm số y = 3x là đường thẳng đi qua các điểm O(0; 0) và A(1; 3)
Hàm số y = ax + b (a \( \ne \) 0 , b \( \ne \) 0)
Đồ thị của hàm số y = ax + b (a \( \ne \) 0, b \( \ne \) 0) là một đường thẳng:
- Cắt trục tung tại điểm có tung độ bằng b;
- Song song với đường thẳng y = ax.
Cách vẽ:
Bước 1. Cho x = 0 thì y = b, ta được điểm M(0; b) trên Oy.
Cho y = 0 thì x = \( - \frac{b}{a}\), ta được điểm N(\( - \frac{b}{a}\); 0) trên Ox.
Bước 2. Vẽ đường thẳng đi qua hai điểm M và N, ta được đồ thị của hàm số y = ax + b
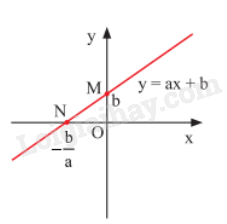
Chú ý: Đồ thị của hàm số y = ax + b còn gọi là đường thẳng y = ax + b.
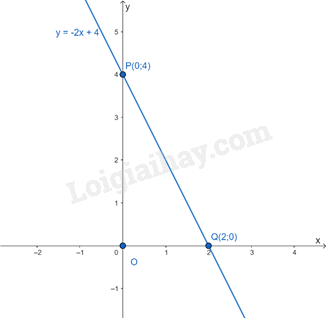
Ví dụ: Cho hàm số y = -2x + 4
Cho x = 0 thì y = 4, ta được điểm P(0;4)
Với y = 0 thì x = 2, ta được điểm Q(2;0)
Đồ thị hàm số y = -2x + 4 là đường thẳng đi qua hai điểm P(0;4) và Q(2;0)