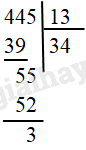Lý thuyết Phép nhân và phép chia số tự nhiên Toán 6 KNTT với cuộc sống — Không quảng cáo

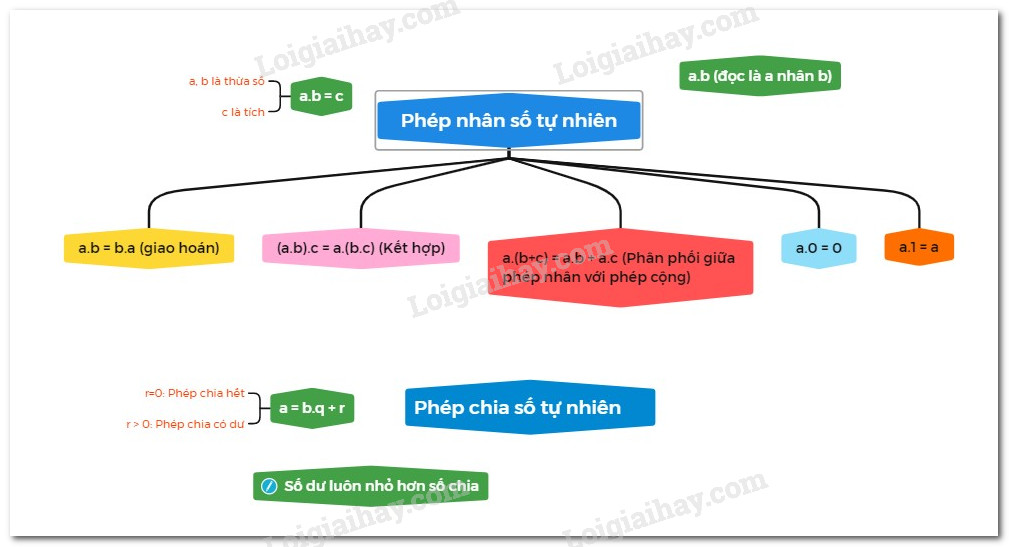
1. Phép nhân số tự nhiên

$a.b = a + a + ... + a$ (Có b số hạng)

$a.b = d$

(thừa số) . (thừa số)  = (tích)

Tính chất của phép nhân:

Giao hoán: $a.b = b.a$

Kết hợp: $\left( {a.b} \right).c = a.\left( {b.c} \right)$

Phân phối của phép nhân đối với phép cộng: $a.\left( {b + c} \right) = a.b + a.c$

Ta hiểu tính chất phân phối ở đây là nếu a nhân với một tổng của b và c thì ta lấy a nhân với b và lấy a nhân với c rồi cộng lại với nhau. Chẳng hạn,$2.(3+5)= 2.3 + 2.5$.

Lưu ý:

1 ) Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không viết dấu nhân giữa các thừa số. Chẳng hạn, $a \times b = a.b = ab$ , $2 \times a = 2.a = 2a$ .

2 ) Trong tính nhẩm ta thường sử dụng các kết quả:

2.5=10

4.25=100

8.125=1000

3) Tích $\left( {ab} \right)c$ hay $a\left( {bc} \right)$ gọi là tích cả ba số a, b, c và viết gọn là $abc$ .

Ví dụ 1: Đặt tính nhân $254.45$

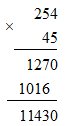
Ví dụ 2: Tính nhẩm 12.25

$12.25 = \left( {3.4} \right).25 = 3.\left( {4.25} \right) = 3.100 = 300$

2. Phép chia hết và phép chia có dư

Chia hai số tự nhiên

Cho hai số tự nhiên $a$  và $b,$  trong đó $b \ne 0$, ta luôn tìm được đúng hai số tự nhiên $q$  và $r$ duy nhất sao cho:

$a = b.q + r$  trong đó  $0 \le r < b$

Nếu $r = 0$ thì ta có phép chia hết :

(số bị chia) : (số chia) = (thương)

Nếu $r \ne 0$ thì ta có phép chia có dư .

(số bị chia) = (số chia) . (thương) + (số dư)

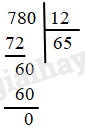
Ví dụ 3: Thực hiện các phép chia sau

a) 780:12

b) 445:13