Lý thuyết Số nguyên tố Toán 6 KNTT với cuộc sống

Lý thuyết Số nguyên tố Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu

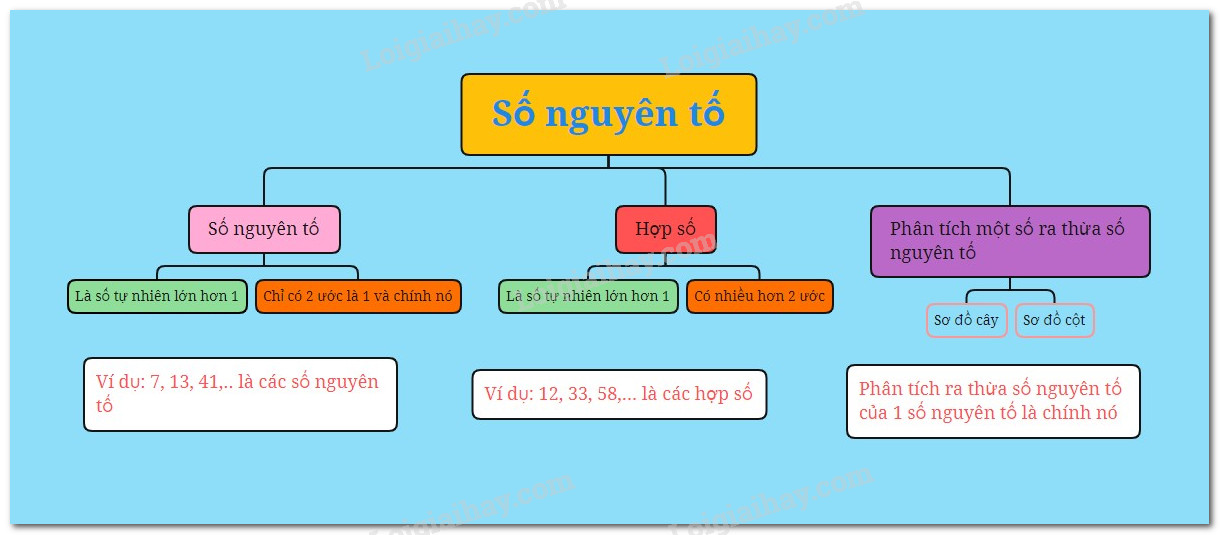
SỐ NGUYÊN TỐ

1. Số nguyên tố và hợp số

+ Số nguyên tố

- Số nguyên tố là số tự nhiên lớn hơn $1,$ chỉ có $2$ ước là $1$ và chính nó.

Ví dụ : Ư$(13) = \{ 13;1\} $ nên $13$ là số nguyên tố.

Nhận xét:

* Cách kiểm tra 1 số là số nguyên tố: Để kết luận số a là số nguyên tố $\left( {a > 1} \right),$

B ước 1 : Tìm số nguyên tố lớn nhất $b$ mà ${b^2} < a$.

Bước 2 : Lấy $a$ chia cho các số nguyên tố từ 2 đến số nguyên tố $b$, nếu $a$ không chia hết cho số nào thì $a$ là số nguyên tố.

+ Hợp số

Hợp số là số tự nhiên lớn hơn $1,$ có nhiều hơn $2$ ước.

Ví dụ : số $15$ có $4$ ước là $1;3;5;15$ nên $15$ là hợp số.

Lưu ý:

+) Số 0 và số 1 không là số nguyên tố cũng không là hợp số.

+) Kiểm tra một số là hợp số: Sử dụng dấu hiệu chia hết để tìm một ước khác 1 và chính nó.

2. Phân tích một số ra thừa số nguyên tố

- Phân tích một số tự nhiên lớn hơn $1$ ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

- Viết các thừa số nguyên tố theo thứ tự từ bé đến lớn, tích các thừa số giống nhau dưới dạng lũy thừa.

Sơ đồ cây:

Bước 1 : Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.

Bước 2 : Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.

Bước 3 : Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.

Bước 4 : Số n bằng tích của các số cuối cùng của mỗi nhánh.

Ví dụ :

Phân tích số 12 ra thừa số nguyên tố bằng sơ đồ cây:

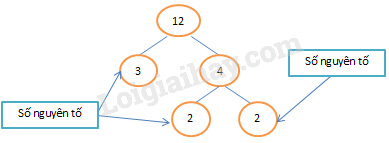
Như vậy $12 = {2^2}.3$

Sơ đồ cột:

Chia số $n$ cho một số nguyên tố (xét từ nhỏ đến lớn ), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng $1.$

Ví dụ : Số $76$ được phân tích như sau:

\[76\]	\[2\]
\[38\]	\[2\]
\[19\]	\[19\]
\[1\]

Như vậy $76 = {2^2}.19$

CÁC DẠNG TOÁN VỀ SỐ NGUYÊN TỐ

1. Viết số nguyên tố hoặc hợp số từ những số cho trước

Phương pháp:

+ Căn cứ vào định nghĩa số nguyên tố và hợp số.

+ Căn cứ vào các dấu hiệu chia hết.

+ Có thể dùng bảng số nguyên tố ở cuối sgk để xác định một số (nhỏ hơn 1000) là số nguyên tố hay không.

Ví dụ: Tìm các số * để được số nguyên tố $\overline {*1} $:

Dấu * có thể nhận các giá trị $\left\{ {1;2;3;4;5;6;7;8;9} \right\}$

+) Với $a=1$ ta có $11$ là số nguyên tố => Thỏa mãn.

+) Với $a=2$ ta có $21$ có các ước $1;3;7;21$ nên $21$ là hợp số=> Loại.

+) Với $a=3$ ta có $31$ là số nguyên tố => Thỏa mãn.

+) Với $a=4$ ta có $41$ chỉ có hai ước là $1;41$ nên $41$ là số nguyên tố => Thỏa mãn.

+) Với $a=5$ ta có $51$ có các ước $1;3;17;51$ nên $51$ là hợp số. Loại

+) Với $a=6$ ta có $61$ là số nguyên tố => Thỏa mãn.

+) Với $a=7$ ta có $71$ là số nguyên tố => Thỏa mãn.

+) Với $a=8$ ta có $81$ có các ước $1;3;9;27;81$ nên $81$ là hợp số. Loại.

+) Với $a=9$ ta có $91$ là có các ước $1;7;13;91$ nên $91$ là hợp số. Loại

Vậy các số nguyên tố là: $11,31,41,61,71$.

2. Chứng minh một số là số nguyên tố hay hợp số.

Phương pháp:

+ Để chứng minh một số là số nguyên tố, ta chứng minh số đó không có ước nào khác $1$ và chính nó.

+ Để chứng minh một số là hợp số, ta chỉ ra rằng tồn tại một ước của nó khác $1$ và khác chính nó. Nói cách khác, ta chứng minh số đó có nhiều hơn hai ước.

Ví dụ:

a) $5$ là số nguyên tố vì nó chỉ có hai ước là $1$ và $5$.

b) $12$ là hợp số vì nó có nhiều hơn hai ước. Cụ thể 12 có các ước là: $1; 2; 3; 4; 6; 12$