Lý thuyết Số thập phân Toán 6 KNTT với cuộc sống

Lý thuyết Số thập phân Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu

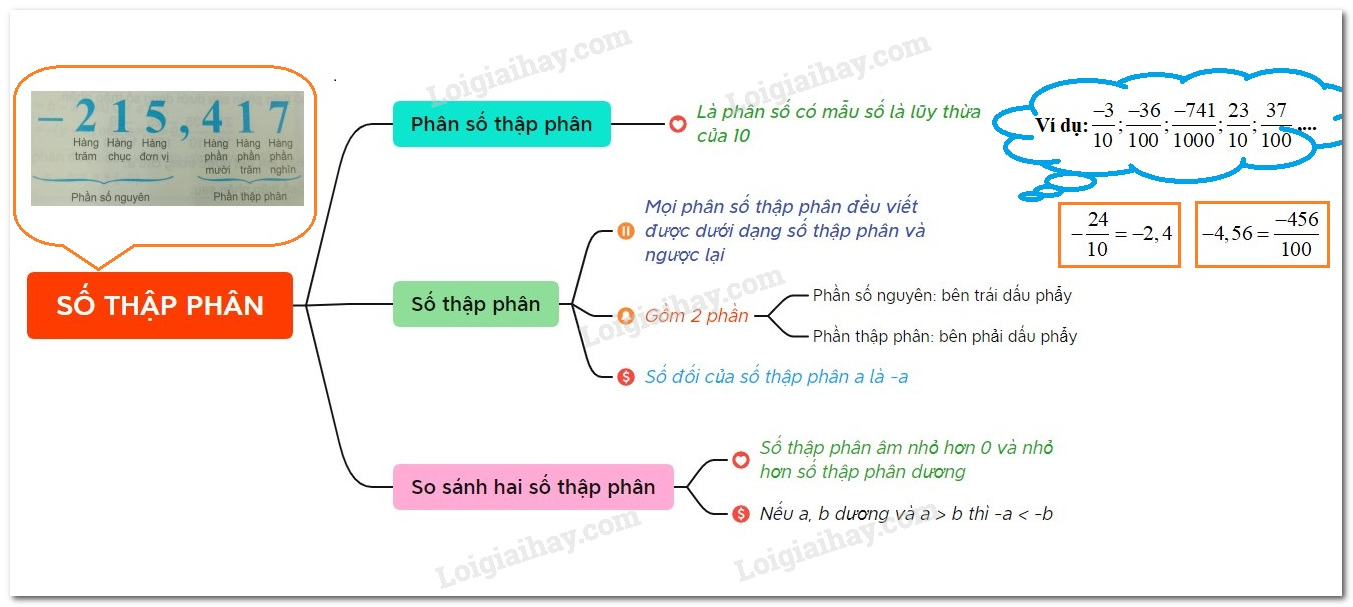
I. Phân số thập phân và số thập phân âm

Phân số thập phân là là phân số mà mẫu là lũy thừa của $10$.

Ví dụ:

$\dfrac{7}{{10}};\dfrac{{ - 15}}{{1000}};...$ là các phân số thập phân.

- Ta viết $ - \dfrac{{15}}{{10}} = - 1,5$ và gọi $ - 1,5$ là số thập phân âm , đọc là “ âm một phẩy năm”.

- Các số $2,3;\,\,0,24;...$gọi là các số thập phân dương , đôi khi còn được viết là $ + 2,3;\,\, + 0,24;...$

- Các số thập phân dương và các số thập phân âm gọi chung là số thập phân.

Nhận xét :

- Mọi phân số thập phân đều viết được dưới dạng số thập và ngược lại.

- Số thập phân gồm hai phần:

+ Phần số nguyên viết bên trái dấu phẩy;

+ Phần thập phân viết bên phải dấu phẩy.

II. Số đối của một số thập phân

Hai số thập phân gọi là đối nhau khi chúng biểu diễn hai phân số thập phân đối nhau.

Ví dụ:

Số đối của $ - 1,5$ là $1,5$.

Số đối của $24,3$ là $ - 24,3$

III. So sánh các số thập phân

a)So sánh 2 số thập phân

Cũng như số nguyên, trong 2 số thập phân khác nhau luôn có một số lớn hơn số kia

*Nếu số thập phân a nhỏ hơn số thập phân b thì ta viết a< b hay b>a

*Số thập phân lớn hơn 0 gọi là số thập phân dương

*Số thập phân nhỏ hơn 0 gọi là số thập phân âm

*Nếu a < b, b < c thì a < c

Cách so sánh 2 số thập phân

* So sánh 2 số thập phân khác dấu: Số thập phân âm luôn nhỏ hơn số thập phân dương

*So sánh 2 số thập phân dương:

Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn

Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng( sau dấu ","), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữu số đó lớn hơn

*So sánh 2 số thập phân âm:

Nếu a< b thì -a> -b