Lý thuyết Số đo góc Toán 6 KNTT với cuộc sống — Không quảng cáo

I. Thước đo góc. Cách đo góc. Số đo góc

a) Thước đo góc

Thước đo góc có dạng nửa hình tròn và được chia đều thành 180 phần bằng nhau, mỗi phần ứng với \({1^o}\).

b) Cách đo góc

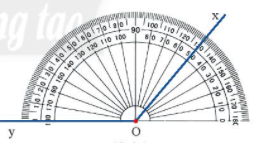
- Bước 1 : Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.

- Bước 2 : Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Oy) đi qua vạch 0 của thước và thước chồng lên phần trong của góc như trên.

- Bước 3 : Xác định xem cạnh còn lại của góc (cạnh Ox) đi qua vạch chỉ số nào trên thước đo góc, ta sẽ được số đo của góc đó.

Ví dụ:

Trong hình bên trên, tia Ox đi qua vạch chỉ số 130, vậy góc xOy có số đo là 130°.

Ta viết \(\widehat {xOy} = {130^o}.\)

c) Số đo góc

Mỗi góc có một số đo. Số đo của góc bẹt là \({180^o}\).

Số đo của mỗi góc không vượt quá \({180^o}\).

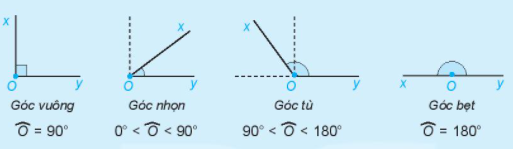
II.Các góc đặc biệt

*Ta có thể so sánh 2 góc dựa vào số đo của chúng

Nếu số đo của góc xOy bằng số đo góc mOn thì góc xOy bằng góc mOn, kí hiệu là \(\widehat {xOy}=\widehat {mOn}\)

Nếu số đo của góc xOy lớn hơn số đo góc mOn thì góc xOy lớn hơn góc mOn, kí hiệu là \(\widehat {xOy}>\widehat {mOn}\)

Nếu số đo của góc xOy nhỏ hơn số đo góc mOn thì góc xOy nhỏ hơn góc mOn, kí hiệu là \(\widehat {xOy}<\widehat {mOn}\)

+Góc nhọn là góc số góc có số đo lớn hơn \(0^0\) và nhỏ hơn  \(90^0\).

+Góc vuông là góc có số đo bằng \(90^0\)

+Góc tù là góc có số đo lớn hơn  \(90^0\) và nhỏ hơn  \(180^0\)

+Góc bẹt là góc có số đo bằng  \(180^0\)