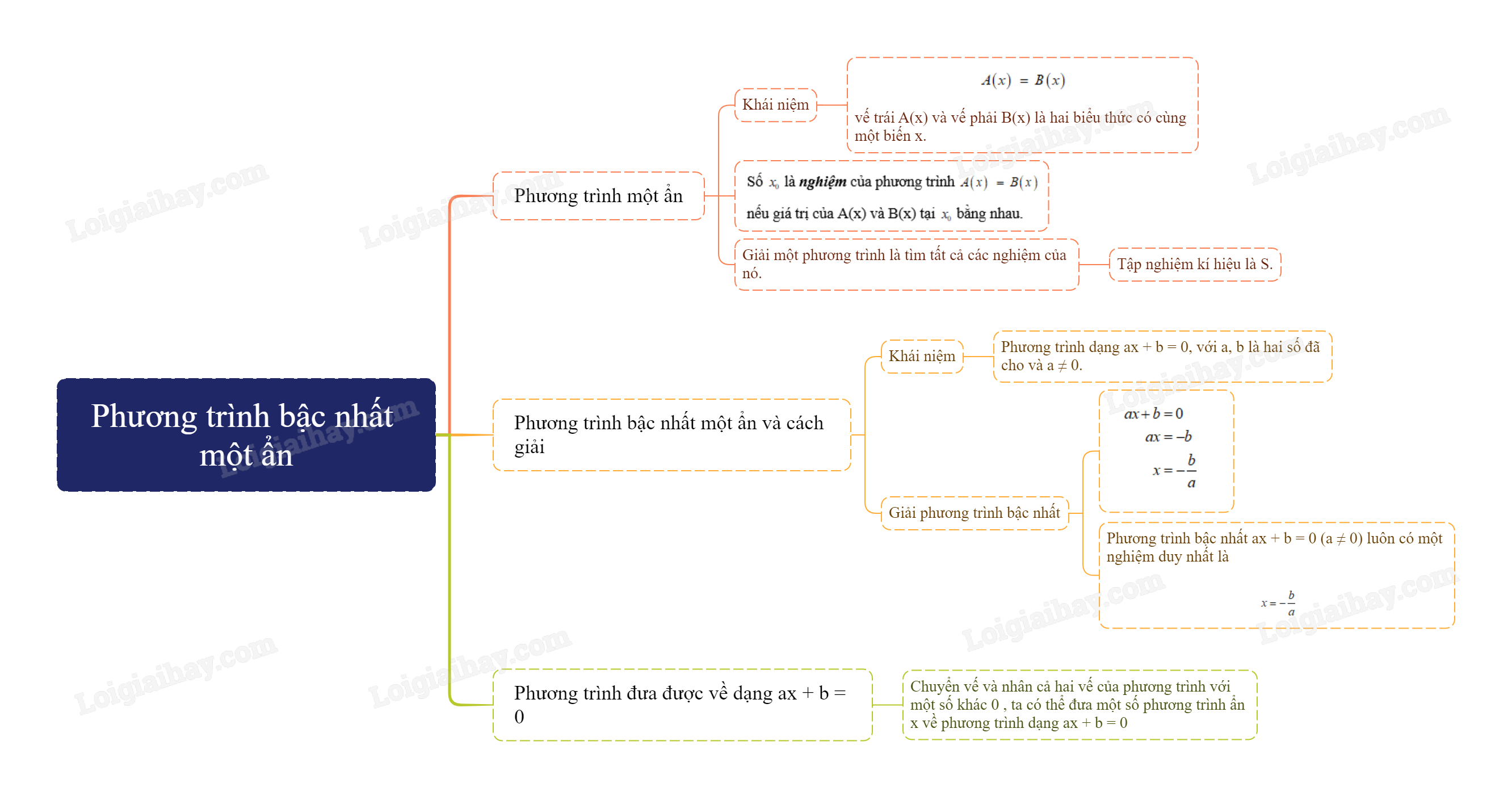
Lý thuyết Phương trình bậc nhất một ẩn SGK Toán 8 - Kết nối tri thức
Phương trình bậc nhất một ẩn là gì?
1. Phương trình một ẩn
Khái niệm:
Một phương trình với ẩn x có dạng \(A\left( x \right){\rm{ }} = {\rm{ }}B\left( x \right)\) , trong đó vế trái A(x) và vế phải B(x) là hai biểu thức có cùng một biến x.
Ví dụ: \(3x{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}2x{\rm{ }} + {\rm{ }}3;{\rm{ }}3x{\rm{ }} = {\rm{ }}5\) là các phương trình ẩn x.
Số \({x_0}\) là nghiệm của phương trình \(A\left( x \right){\rm{ }} = {\rm{ }}B\left( x \right)\) nếu giá trị của A(x) và B(x) tại \({x_0}\) bằng nhau.
Ví dụ: \(x{\rm{ }} = {\rm{ }}2\) là nghiệm của phương trình \(2x{\rm{ }} = {\rm{ }}x{\rm{ }} + {\rm{ }}2\) vì thay \(x{\rm{ }} = {\rm{ }}2\) vào phương trình, ta được 2.2 = 2 + 2
Giải một phương trình là tìm tất cả các nghiệm của nó.
Chú ý: Tập hợp tất cả các nghiệm của một phương trình được gọi là tập nghiệm của phương trình đó và kí hiệu là S.
Ví dụ: Giải phương trình: \(3x + 6 = 0\)
Ta có: \(3x + 6 = 0 \Leftrightarrow 3x = - 6 \Leftrightarrow x = - 2\)
Vậy tập nghiệm của phương trình là S = {-2}
2. Phương trình bậc nhất một ẩn và cách giải
Khái niệm: Phương trình dạng ax + b = 0, với a, b là hai số đã cho và \(a \ne 0\) , được gọi là phương trình bậc nhất một ẩn x.
Cách giải:
Phương trình bậc nhất ax + b = 0 ( \(a \ne 0\) ) được giải như sau:
\(\begin{array}{c}ax + b = 0\\ax = - b\\x = - \frac{b}{a}\end{array}\)
Phương trình bậc nhất ax + b = 0 ( \(a \ne 0\) ) luôn có một nghiệm duy nhất là \(x = - \frac{b}{a}\) .
Ví dụ: Giải phương trình: \(3x + 11 = 0\)
Ta có: \(3x + 11 = 0 \Leftrightarrow 3x = - 11 \Leftrightarrow x = - \frac{{11}}{3}\)
Vậy nghiệm của phương trình là \(x = - \frac{{11}}{3}\) .
3. Phương trình đưa được về dạng ax + b = 0
Bằng cách chuyển vế và nhân cả hai vế của phương trình với một số khác 0, ta có thể đưa một số phương trình ẩn x về phương trình dạng ax + b = 0 và do đó có thể giải được chúng.
Ví dụ: Giải phương trình: \(7x{\rm{ }}-{\rm{ }}\left( {2x{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}5\left( {x{\rm{ }}-{\rm{ }}2} \right)\)
\(\begin{array}{c}11x{\rm{ }}-{\rm{ }}\left( {2x{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ 6}}\left( {x{\rm{ }}-{\rm{ }}2} \right)\\11x - 2x - 3 = 6x - 12\\11x - 2x - 6x = - 12 + 3\\3x = - 9\\x = \frac{{ - 9}}{3}\\x = - 3\end{array}\)
Vậy nghiệm của phương trình là x = -3